915F.Imbalance Value of a Tree（并查集+树上信息统计）

您将得到由n个顶点组成的树T。 每个顶点上都有一个数字。 写在顶点i上的数字是ai。 让我们将函数I（x，y）表示为在连接顶点x和y的简单路径上ai的最大值和最小值之间的差。

您的任务是计算。

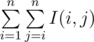
题解：

考虑单独算每个点的贡献。

把点权转化为边权，对于最大值的贡献，把每条边的边权设为两个点点权的较大值。然后将所有边从小到大排序，依次枚举，枚举的时候用并查集维护，每条边的贡献就是所连接的两个点的连通块点数乘积。

算最小值的贡献同理。

//定义两点间的边权为两点的最大值
//然后将每条边从小到大排序
//用并查集合并
//每条边的贡献是当前所连接的两个连通块内的点数之积
//最小值同理
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+100;
int n,a[maxn];
struct node {
    int u,v,w;
    bool operator < (const node &r) const {
        return w<r.w;
    }
}edge[2][maxn];
int father[maxn],num[maxn]; 
int findfather (int x) {
    int a=x;
    while (x!=father[x]) x=father[x];
    while (a!=father[a]) {
        int z=a;
        a=father[a];
        father[z]=x;
    }
    return x;
}
void Union (int x,int y) {
    x=findfather(x);
    y=findfather(y);
    if (x!=y) {
        father[x]=y;
        num[y]+=num[x];
        num[x]=0;
    }
}
int main () {
    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%d",a+i);
    for (int i=1;i<n;i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        edge[0][i].u=u;
        edge[0][i].v=v;
        edge[0][i].w=max(a[u],a[v]);
        edge[1][i].u=u;
        edge[1][i].v=v;
        edge[1][i].w=min(a[u],a[v]);
    }
    long long ans=0;
    sort(edge[0]+1,edge[0]+n);
    for (int i=1;i<=n;i++) father[i]=i,num[i]=1;
    for (int i=1;i<n;i++) {
        int u=edge[0][i].u;
        int v=edge[0][i].v;
        ans+=1ll*edge[0][i].w*num[findfather(u)]*num[findfather(v)];
        Union(u,v);
    }
    for (int i=1;i<=n;i++) father[i]=i,num[i]=1;
    sort(edge[1]+1,edge[1]+n);
    for (int i=n-1;i>=1;i--) {
        int u=edge[1][i].u;
        int v=edge[1][i].v;
        ans-=1ll*edge[1][i].w*num[findfather(u)]*num[findfather(v)];
        Union(u,v);
    }
    printf("%lld
",ans);
}