题目描述:

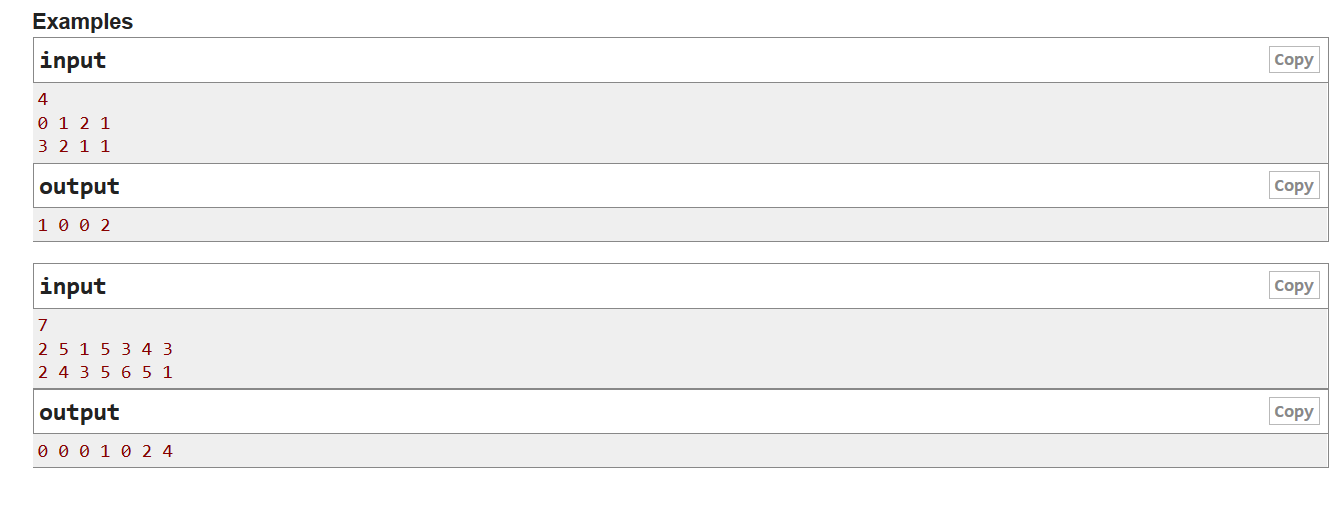
知识点:
lower_bound和uper_bound
lower_bound(起始地址,结束地址,要查找的数值) 返回的是数值 第一个 出现的位置。
upper_bound(起始地址,结束地址,要查找的数值) 返回的是数值 最后一个 出现的位置。
binary_search(起始地址,结束地址,要查找的数值) 返回的是是否存在这么一个数,是一个bool值。
lower_bound(val):返回容器中第一个值【大于或等于】val的元素的iterator位置。
upper_bound(val): 返回容器中第一个值【大于】val的元素的iterator位置
使用:
1 int low=lower_bound(t.begin(),t.end(),5)-t.begin(); 2 int upp=upper_bound(t.begin(),t.end(),5)-t.begin();
思路:
题目是说要让数组a的每一位与b中某一位相加取余后最小,找规律可得
a 对应b的“最好选择元素”的优先级为
0 0 1 2 ... n-1
1 n-1 0 1 ... n-2
2 n-2 n-1 0 ... n-3
...
n-1 1 2 3 ... 0
刚开始做法是真的列了一个大数组从0到200000,读入b的时候就直接把数字存到index对应的位置,如b[n]=n,然后根据不同的a[i]遍历整个b数组,结果超时
第二次把不用b那么大的数组,b中只存b[i],对b排序,对每个a[i]遍历b数组,因为b中对应a[i]最优先的数应为n-a[i]。在b中查找,如果找到,数字用掉并标记为-1;若没找到,按算法应返回的是不超过b的最后一个元素,此时将位置+1即可选取到次优先的a[i]对应的数,当然要选择大于等于0的数,即为使用的。结果超时
第三次不用标记-1,改用listr直接remove,想着是删除元素list应该比vector要快一点,结果超时
第四次想到既然排好序了,二分吧,刚好可以用lower_bound符合语义。结果超时
最后上网搜题解,用multiset的lower_bound,要更快。。。好像set的内部实现是平衡二叉树,所以更快?
不过最后提醒了我,既然排好序了,就该想到二分来提速(O(log n)),而不是傻傻的遍历一遍又一遍(O(n)).
下面是代码:
1 #include <iostream> 2 #include <algorithm> 3 #include <vector> 4 #include <set> 5 #define max_n 200005 6 using namespace std; 7 int n; 8 vector<int> a; 9 multiset<int> b; 10 11 int main() 12 { 13 cin >> n; 14 int nums; 15 for(int i = 0;i<n;i++) 16 { 17 cin >> nums; 18 a.push_back(nums); 19 } 20 for(int i = 0;i<n;i++) 21 { 22 cin >> nums; 23 b.insert(nums); 24 } 25 for(auto i = a.begin();i!=a.end();i++) 26 { 27 int num = n-*i; 28 //cout << "num " << num << endl; 29 set<int>::iterator j; 30 //for(j = b.begin();*j<num&&j!=b.end();j++); 31 j = b.lower_bound(num); 32 if(j!=b.end()&&(*j==num||*j>num)) 33 { 34 *i = (*i+*j)%n; 35 } 36 else if(j==b.end()) 37 { 38 j=b.begin(); 39 *i=(*i+*j)%n; 40 } 41 //cout << "b " << b[j] << endl; 42 b.erase(j); 43 } 44 for(auto i = a.begin();i!=a.end();i++) 45 { 46 cout << *i << " "; 47 } 48 return 0; 49 }