FJUToj-3281-外传：魔王打工记（一）

外传：魔王打工记（一）

TimeLimit:1000MS  MemoryLimit:128MB

64-bit integer IO format:%lld

 

Problem Description

话说Home_W大魔王手下有四大天王： 首席战神——赛文斯，SoftWork首席科学家——布莱克，首席军师——金金金，首席狙击手——超无聊，首席苦力——小明。

    然而，这些部下个个都是饭桶，把Home_W都快吃穷。虽然Home_W嘴上说：打工是不可能打工的，这辈子不可能打工的。烧杀抢又不会做，就只有当正义的魔王这种东西，才能维持的了生活的体面，进了魔王堡感觉像回家一样，在魔王堡的感觉比家里感觉好多了！里面个个都是人才，说话又好听，我超喜欢里面的！”但实际上，Home_W在背地里伪造了各种身份，偷偷地做一些兼职以维持生计。

    现在Home_W刚升入国家统计局工作，统计局里刚给他分配报酬1e RMB的一项工作：

给出N个整数a1,a2,a3,……，a_N,问：对于任意的L,R。求序列a_L,a_L+1……a_R的方差乘（R-L+1）²

其中方差的公式如下：

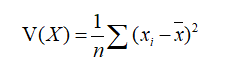
Home_W在接到工作后熟练敲起了代码，只见他摸上键盘的一瞬间天黑地暗，大地都在颤抖，星辰都在闪烁，不到一分钟就算完了。办公室里的无不起立鼓掌，领导也对其刮目相看，额外奖励了他价值1e9+7 RMB的破坏公物罚单一张。

Input

单组数据

开头是一个整数N,q代表N个数字，q次询问.N,q<=100,000

接下来有n个数a1,a2,a3,……an  ,（0<=ai<=10000）

再接下来q行，每行包含两个整数L,R. (1<=L<=R<=N)

Output

对于每个查询输出一个整数，代表方差乘（R-L+1）²

SampleInput

10 10
6 1 3 0 4 5 0 7 7 4
8 10
2 4
1 3
5 8
7 9
4 10
1 9
4 6
1 6
9 10

SampleOutput

18
14
38
104
98
356
576
42
161
9

题解：

方差

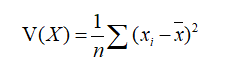
  且 n = (R-L+1)  平均值x为sum/n

所以方差*（R-L+1）化简为

  result(x) = 1/n*∑((xi-sum/n)^2)*n^2
          =n*∑((xi-sum/n)^2)
          =n*∑((xi-∑xi/n)^2)
          =n*∑(xi^2-2*xi*∑xi/n+(∑xi)^2/n^2))
          =n*∑(xi^2)-2*(∑xi)^2+(∑xi)^2
          =n*∑(xi^2)-(∑xi)^2

所以输出的值就是

　　　　　　n*∑(xi^2)-(∑xi)^2（L<=i<=R）

如果每次采用查询都采用暴力必然导致超时，所以在输入时就要进行记录，计算出前缀和∑xi以及前缀的平方和∑(xi^2)，这样要用这两个数据时时间复杂度就是O（1）

附上代码：

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <math.h>
#include <string.h>
#include <stack>
#define ll long long
using namespace std;
ll sum1[100005],sum2[100005];
int main(void)
{
    ll l,r,n,q,x,sum=0;
    cin>>n>>q;
    sum1[0]=(ll)0;
    sum2[0]=(ll)0;
    for(ll i=1;i<=n;i++)
    {
        cin>>x;
        sum2[i]=sum2[i-1]+x;
        sum1[i]=x*x+sum1[i-1];
    }
    while(q--)
    {
        cin>>l>>r;
        cout<<(r-l+1)*(sum1[r]-sum1[l-1])-(sum2[r]-sum2[l-1])*(sum2[r]-sum2[l-1])<<endl;
    }
    return 0;
}

题解参考：https://www.cnblogs.com/qq136155330/p/9038664.html