1. 数学分析
1) 画直线的问题
本来我以为画直线会很容易,随便拿个直线公式,遍历X求Y画出来不就完了么,但事实并非如此。以2D直线为例,因为3D直线也只是多引入了个Z坐标而已。关键的问题:我们在数学中所学的直线是基于实数域的,而在计算机屏幕上,所画的直线是基于正整数域的,可以想象这么一个情形,在直线的某一点X=1,Y=0.01时,在屏幕上如何画呢?下图对比了实数域的直线,与基于正整数域的直线:
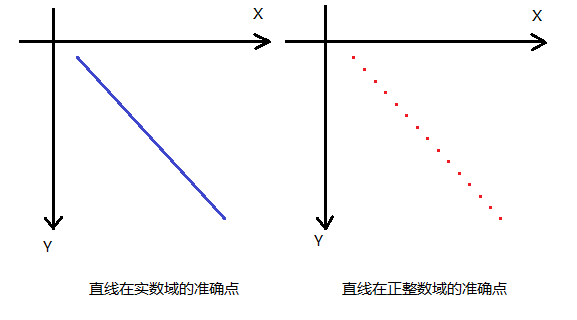
为什么直线在正整数域是不连续的呢,还记得斜率的的定义么:斜率m = dy / dx = (y1 - y0) / (x1 - x0)
这意味着当X坐标增加1,则Y坐标就增加m。这就是会出现上述情况的根本原因。
2) Bresenham算法
该算法由Bresenham在1965年发明,它到底做了什么事呢?其实想法很简单,就是每X移动一个像素,则考虑Y应该是如何移动。为什么我们要关注Bresenham算法呢,我们发现,这种算法实际只做了加减法,是非常适合计算机运算的,这种算法的速度是相当快的。
该算法把直线分为两种:一种是斜率<1的线,即近X轴线。另一种是斜率>1的线,即近Y轴线。
我们以近X轴直线为例,如图:
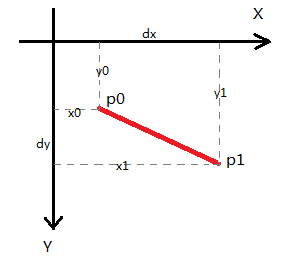
Bresenham算法的核心就是,当X加1后,如何决定Y的移动。显然可见,近X轴直线的dy<dx。所以一个直观的想法是,保存一个误差累计变量,每当X加1,误差变量便累计增加一个dy。当累计误差小于等于dx时,Y不动,当累计的误差大于dx时,Y加1,同时把累计误差减掉一个dx。这样,算法将不停的将光栅线与实际线之间的误差减到最小。
2. 函数实现
这里给出一个例子,实现了上面的算法,但只限近X轴并且是从左上往右下画的,可以很清楚的看到实现的逻辑。通用的画线在源码中已实现,可以下载获取。
int dx = x1 - x0;
int dy = y1 - y0;
int error = 0;
if (dx > dy) // 近X轴
{
for (int x = x0, y = y0; x<= x1; ++x)
{
DrawPixel(x, y, color);
error += dy; // 累计误差
if (error > dx)
{
error -= dx;
++y;
}
}
}
针对所有情况的完整代码如下,其中在误差的计算方面进行了一些优化,起始值更居中,而不是写死的0。
int _CPPYIN_3DLib::DrawLine(int x0, int y0, int x1, int y1, DWORD color)
{
int x, y, dx, dy, dx2, dy2, xstep, ystep, error, index;
x = x0;
y = y0;
dx = x1 - x0;
dy = y1 - y0;
if (dx >= 0) // 从左往右画
{
xstep = 1; // x步进正1
}
else // 从右往左画
{
xstep = -1; // x步进负1
dx = -dx; // 取绝对值
}
if (dy >= 0) // 从上往下画
{
ystep = 1; // y步进正1
}
else // 从下往上画
{
ystep = -1; // y步进负1
dy = -dy; // 取绝对值
}
dx2 = dx << 1; // 2 * dx
dy2 = dy << 1; // 2 * dy
if (dx > dy) // 近X轴直线
{
error = dy2 - dx;
for (index = 0; index <= dx; ++index)
{
DrawPixel(x, y, color);
if (error >= 0)
{
error -= dx2;
y += ystep;
}
error += dy2;
x += xstep;
}
}
else // 近Y轴直线
{
error = dx2 - dy;
for (index = 0; index <= dy; ++index)
{
DrawPixel(x, y, color);
if (error >= 0)
{
error -= dy2;
x += xstep;
}
error += dx2;
y += ystep;
}
}
return 1;
}
3. 源码下载
这个示例使用该函数,每帧在窗口中画500条随机颜色的直线,截图如下:

项目源代码下载:>>点击进入下载页<<
4. 补充更新
画直线还有一些算法,速度有的更快,如:
Run-Slicing
Symmetric Double Step
Quadruple Step
如果有时间我会一一实现,如果读者已经实现,请留言分享,谢谢。