分块查找(索引表查找)
分块查找是折半查找和顺序查找的一种改进方法,折半查找虽然具有很好的性能,
但其前提条件时线性表顺序存储而且按照关键码排序,这一前提条件在结点树很
大且表元素动态变化时是难以满足的。而顺序查找可以解决表元素动态变化的要求,
但查找效率很低。如果既要保持对线性表的查找具有较快的速度,又要能够满足表
元素动态变化的要求,则可采用分块查找的方法。分块查找的速度虽然不如折半查找算法,
但比顺序查找算法快得多,同时又不需要对全部节点进行排序。当节点很多且块数很大时,
对索引表可以采用折半查找,这样能够进一步提高查找的速度。
分块查找由于只要求索引表是有序的,对块内节点没有排序要求,因此特别适合于节点动态变化
的情况。当增加或减少节以及节点的关键码改变时,只需将该节点调整到所在的块即可。
在空间复杂性上,分块查找的主要代价是增加了一个辅助数组。
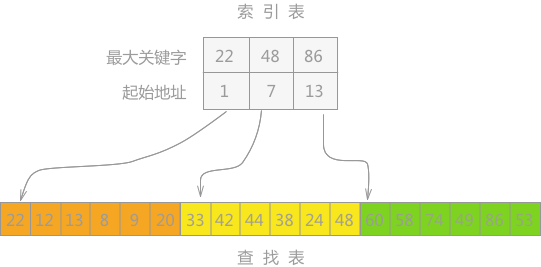
由上图我们可以看出,这个表中有18个元素,我们将其分为了三个块,每个块有6个元素。
使用分块查找的要求:
1:索引表必须要有序,而每一个索引块不必有序;
2:第一个索引块中的任意元素必须小于第二个索引块中的任意元素,第二个索引块中的任意
元素必须小于第三个索引块中任意元素。。。。。依次类推;
步骤:
1:建立辅助数组,即索引表。
2:找出每个索引块中的最大元素,依次存入到索引表中。
3:在索引表中找到key所存在的索引块(目标索引块)。(顺序查找)。
4:在目标索引块中查找key(顺序查找),若存在输出对应的下标。
代码:
#include<iostream> using namespace std; int fenkuai_search(int A[],int n,int m,int key) { int max=0;//用来记录每个索引块中的最大值 int M=0; int B[n/m-1];//建立索引表数组; int j=0; for(int i=0;i<n;i++)//寻找每一个索引块中的最大值; { M++; if(M<=m&&A[i]>max) max=A[i]; if(M==m) { B[j]=max; j++; M=0; } } for(int i=0;i<n/m;i++)//在索引表中查找索引块 { if(key<=B[i])//找到对应的索引块 { for(int x=i*m;x<(i+1)*m;x++)//在对应的索引块中查找key; { if(A[x]==key) return x; } } } return -1; } int main()//举例用法 { int A[]={22,12,13,8,9,20,33,42,44,38,24,48,60,58,74,49,86,53}; int key; cin>>key; int x=fenkuai_search(A,18,3,key); if(x!=-1) cout<<key<<"元素所在的位置为:"<<x; else cout<<"该数组中没有该元素"; return 0; }