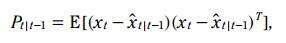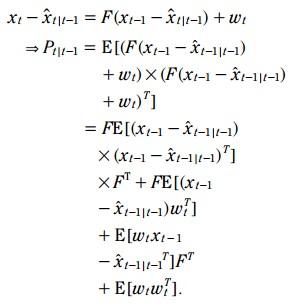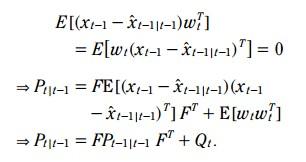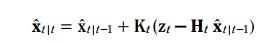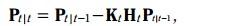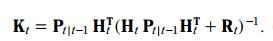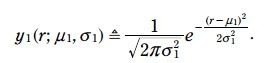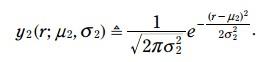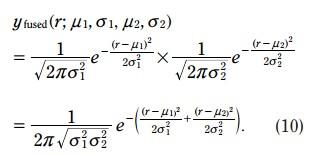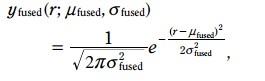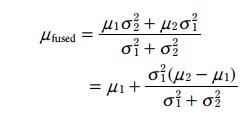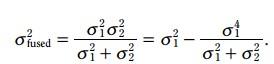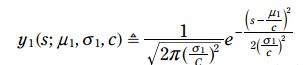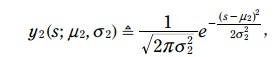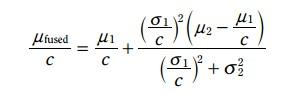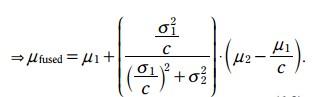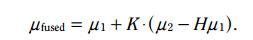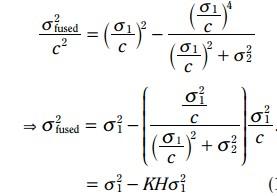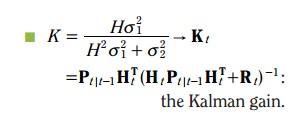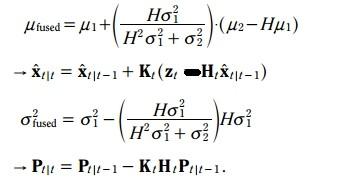[Math]理解卡尔曼滤波器 (Understanding Kalman Filter) - 走看看

1. 卡尔曼滤波器介绍

卡尔曼滤波器的介绍，见 Wiki

这篇文章主要是翻译了 Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation

感谢原作者。

如果叙述有误，欢迎指正！

2. 基本模型

2.1 系统模型

卡尔曼滤波模型假设k时刻的真实状态是从(k − 1)时刻的状态演化而来，符合下式：

(1)

Fk 是作用在 Xk−1 上的状态变换模型（/矩阵/矢量）。
Bk 是作用在控制器向量uk上的输入－控制模型。
Wk 是过程噪声，并假定其符合均值为零，协方差矩阵为Qk的多元正态分布。

(2)

2.2 测量模型

时刻k，对真实状态 xk的一个测量zk满足下式:

(3)

其中Hk是观测模型,它把真实状态空间映射成观测空间，vk 是观测噪声，其均值为零，协方差矩阵为Rk,且服从正态分布。

(4)

初始状态以及每一时刻的噪声{x0, w1, ..., wk, v1 ... vk} 都认为是互相独立的.

卡尔曼滤波要做的是：

已知：

系统的初始状态 x0
每个时间的测量 Z
系统模型和测量模型

求解：

状态x随着时间变化而产生的值

3. 预测与更新

3.1 预测方程

预测是这样一个问题：

已知:

上一个状态的更新值
上一个状态的更新值和真实值之间的误差

求解：

这一个状态的预测值
这一个状态的预测值和真实值之间的误差

过程包括两个方面：

一、由上一个更新值 Xk-1|k-1 预测这一个预测值 Xk|k-1

二、由上一个更新值和真实值之间的误差 Pk-1|k-1 预测下一个预测值和真实值之间的误差 Pk|k-1

具体来说，就是以下两个方程。

(预测状态) (5)

(预测估计协方差矩阵) (6)

这里：

Xk-1|k-1 这种记法代表的是上一次的更新值，后面一个 k-1可以看做 Zk-1，也就是上一次经过对比Zk-1(实际就是更新)之后所估计出的状态Xk-1。

Xk|k-1 这种记法代表这一次的预测值，同理于刚才的介绍，经过上一次Zk-1之后所估计出的状态Xk。

预测公式-预测状态
也就是公式(5)，可以直接由系统模型导出。

预测公式-协方差矩阵：

P代表着估计误差的协方差，代表着一种 confidence ，比如先验估计误差(预测值与真实值之间误差)的协方差

注：

方差有两种形式

协方差的定义：

如果说方差是用来衡量一个样本中，样本值的偏离程度的话。协方差就是用来衡量两个样本之间的相关性有多少，也就是一个样本的值的偏离程度，会对另外一个样本的值偏离产生多大的影响，协方差是可以用来计算相关系数的，相关系数P=Cov(a.b)/Sa*Sb, Cov(a.b)是协方差， Sa Sb 分别是样本标准差。【可以参考另一篇博客《理解协方差》】

cov(x,y)
= E( (x-u)(y-v)' )
= E(xy' - xv' - uy' + uv')
= E(xy') - E(xv') - E(uy') + E(uv')
= E(xy') - uv' - uv' + uv'
= E(xy') - uv'

比较(5)和(1), 相减：

由于状态估计误差和系统噪声是不相关的

注：

如果随机变量 x和y是不相关的，那么

Cov(x,y) = 0
=> E( (x-ex)(y-ey)' ) = 0
=> E(xy') - ex*ey' = 0

如果 ex 和ey为0 => E(x,y') = 0 就像上面的情况，误差和噪声都服从正态分布，所以期望都是0 .

独立的充要条件：P(xy) = P(x)P(y)

3.2 更新方程

更新过程实际上就是一下问题：

已知：

由上一个更新值得到的当前的预测值。
当前的观测值
观测模型

求解：

融合了预测值和观测的更新值
由预测值的估计误差得到更新值的估计误差

更新方程如下：

其中K称为kalman增益，就像一个补偿，决定着预测值应该变化多少幅度，才能变成更新值。

先看一个简单的例子，从这个例子中来推导出这三个方程。

3.3 简单的例子

3.3.1 举例

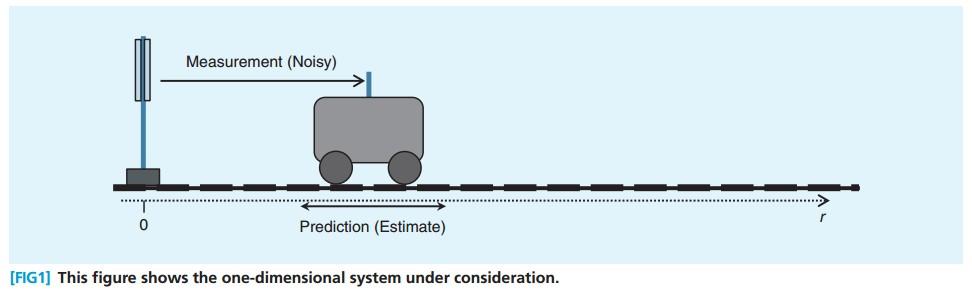
有一个直线轨道，轨道上有一个火车，从火车站出发，在t时刻，火车想要知道自己距离火车站的位置，可以有两个信息来源：

根据 t-1时刻的状态信息，以及一些控制信息来推断，状态包括 t-1时刻的位置、速度等，控制信息包括司机刹车、加速等等。
根据 t时刻的测量数据来推断，这里假设车上有一个声波发射器，可以探测到发射到火车站需要多少时间，进而得到离车站的距离。

要想得到一个比较好的结果，显然不能只依靠某一种方法来推断，而 Kalman Filter的方法是：

首先，利用t-1时刻进行推断，这一步叫预测。
然后，利用t时刻的measurement 也可以推断，使用这个推断对预测进行校正，这一步叫更新。

3.3.2 火车位置 - 预测

t=0的时候，火车状态如 Figure.2 ，这时候，火车的位置是比较准确的。

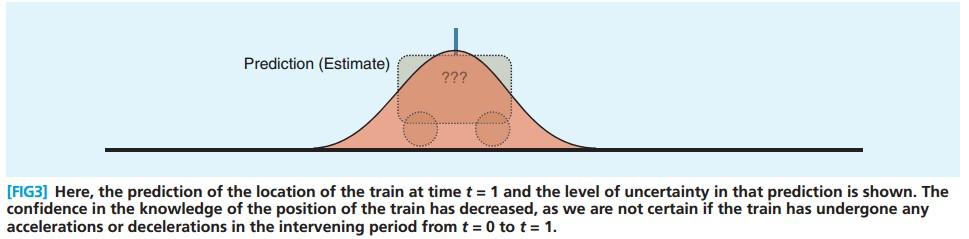
t=1的时候，火车的预测状态如 Figure.3 可以看到，位置的方差变大了。

火车的预测主要遵循式(1)，而预测的方差在不断变大,也就是说预测的准确度在下降, 这是由累积误差 w 导致的。

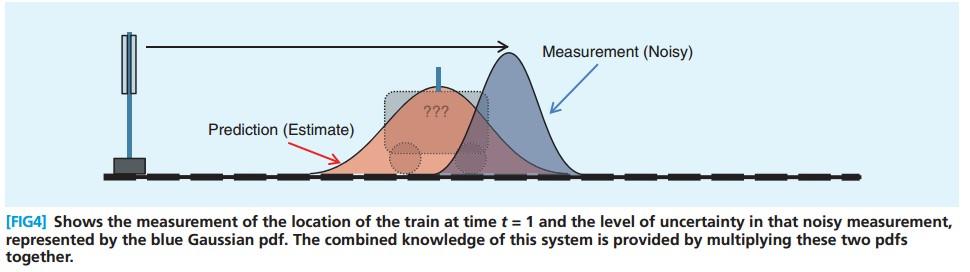
3.3.3 火车位置 - 测量

t=1 的时候，我们还有 measurement ，同样可以推断火车的位置，见下图中的蓝色的pdf

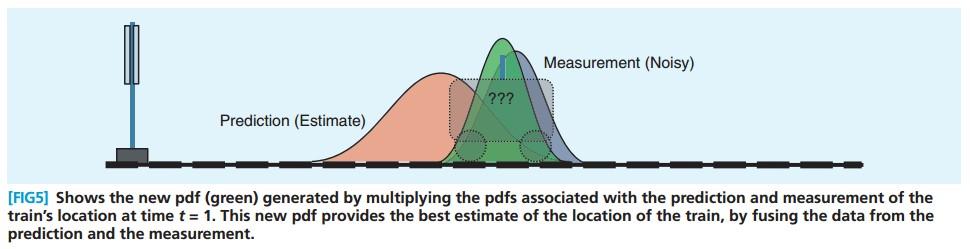
3.3.4 火车位置 - 更新

将两个pdf相乘，得到下图中的绿色pdf，绿色pdf中较高的位置，意味着预测和测量对这个位置都比较支持。

这里有一个高斯分布的一个重要性质就是，两个高斯分布的乘积还是高斯分布。

This is critical as it permits an endless number of Gaussian pdfs to be multiplied over time, but the resulting
function does not increase in complexity or number of terms; after each time epoch the new pdf is fully represented by a Gaussian function. This is the key to the elegant recursive properties of the Kalman filter。

3.3.5 推导更新方程

红色的pdf是预测的火车位置, 方程如下：

蓝色的pdf是测量的火车位置, 方程如下：

绿色的pdf二者融合的或者位置, 方程如下：

写成如下形式：

这里：

这两个式子，就是kalman滤波的更新方程

但是，这只是一个很特殊的例子，因为这里假设预测和测量都是采用同样的坐标系

更现实的情况是二者需要统一到一个 domain 中

比如上面所举的例子中：

预测的时候，预测值是用米作为单位的。
但是当测量的时候，测量得到的值是用声波经过的秒数作为单位的。

必须先要把两个量统一到同一个domain才能进行融合。

比如上式子中， y2 (measurement)实际是声波传递时间的一个正态分布，也就是说单位是秒。

一般做法是把
预测值 => 测量值

y1就变成：

y2不变：

这样两个坐标系都在 mesaurement domain 了。

两个pdf所在坐标系的横轴都是表示时间，而且以秒为单位了。

`
统一domain之后，更新方程就有了如下形式

3.3.5.1 期望更新方程:

将

H = 1/c

K = 代入，得到

这里的H就相当于观测方程中的H， K就是卡尔曼增益。

3.3.5.2 方差更新方程:

类似地，融合之后的方差更新变成了

4. 总结

各个变量对应的情况如下：

最终的更新方程

5. 实现

Talk is cheap, show me the code.

%本例子从百度文库中得到， 稍加注释
clear
N=200;%取200个数

%% 生成噪声数据 计算噪声方差
w=randn(1,N); %产生一个1×N的行向量，第一个数为0，w为过程噪声（其和后边的v在卡尔曼理论里均为高斯白噪声）
w(1)=0;
Q=var(w); % R、Q分别为过程噪声和测量噪声的协方差(此方程的状态只有一维，方差与协方差相同) 

v=randn(1,N);%测量噪声
R=var(v);

%% 计算真实状态
x_true(1)=0;%状态x_true初始值
A=1;%a为状态转移阵，此程序简单起见取1
for k=2:N
    x_true(k)=A*x_true(k-1)+w(k-1);  %系统状态方程，k时刻的状态等于k-1时刻状态乘以状态转移阵加噪声（此处忽略了系统的控制量）
end


%% 由真实状态得到测量数据， 测量数据才是能被用来计算的数据， 其他都是不可见的
H=0.2;
z=H*x_true+v;%量测方差，c为量测矩阵，同a简化取为一个数


%% 开始 预测-更新过程

% x_predict: 预测过程得到的x
% x_update:更新过程得到的x
% P_predict:预测过程得到的P
% P_update:更新过程得到的P

%初始化误差 和 初始位置
x_update(1)=x_true(1);%s(1)表示为初始最优化估计
P_update(1)=0;%初始最优化估计协方差

for t=2:N
    %-----1. 预测-----
    %-----1.1 预测状态-----
    x_predict(t) = A*x_update(t-1); %没有控制变量
    %-----1.2 预测误差协方差-----
    P_predict(t)=A*P_update(t-1)*A'+Q;%p1为一步估计的协方差，此式从t-1时刻最优化估计s的协方差得到t-1时刻到t时刻一步估计的协方差

    %-----2. 更新-----
    %-----2.1 计算卡尔曼增益-----
    K(t)=H*P_predict(t) / (H*P_predict(t)*H'+R);%b为卡尔曼增益，其意义表示为状态误差的协方差与量测误差的协方差之比(个人见解)
    %-----2.2 更新状态-----
    x_update(t)=x_predict(t)  +  K(t) * (z(t)-H*x_predict(t));%Y(t)-a*c*s(t-1)称之为新息，是观测值与一步估计得到的观测值之差，此式由上一时刻状态的最优化估计s(t-1)得到当前时刻的最优化估计s(t)
    %-----2.3 更新误差协方差-----
    P_update(t)=P_predict(t) - H*K(t)*P_predict(t);%此式由一步估计的协方差得到此时刻最优化估计的协方差
end

%% plot
%作图，红色为卡尔曼滤波，绿色为量测，蓝色为状态
%kalman滤波的作用就是 由绿色的波形得到红色的波形， 使之尽量接近蓝色的真实状态。
t=1:N;
plot(t,x_update,'r',t,z,'g',t,x_true,'b');

6. Reference

Wiki-卡尔曼滤波器

Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation

Wiki-协方差矩阵