这一讲主要介绍了神经网络,基本内容之前如果学习过Andrew的Machine learning应该也都有所了解了。不过这次听完这一讲后还是有了新的一些认识。
计算图 Computational graph
之前没有体会到计算图的强大,今天听Serena讲解后,有一种豁然开朗的感觉。 总的来说,有一些很复杂的表达式,如果直接使用它对变量求导,虽然也能得到一个显式的表达,但可能会牵扯到非常复杂的展开、求导等一系列操作。如果换种方式,把这个式子里的基本运算,通过计算图的方式表示出来,用节点来表示一个基本运算,如 +、*、max等。那么我们从结尾出发,不断地在当前的节点上对前面的变量进行求导,这个求导过程往往非常简单,然后根据链式法则,不断“向后”传播,就可以得到整个式子关于输入变量的导数。这个思想也正是神经网络的精髓所在。
值得注意的是,我们可以根据自己的需要选择性地合并一些节点,比如像sigmoid函数,非常常见,而且我们也能够给出它的微分的显式表达,这时候就没有必要冗余地去列举sigmoid函数里的每一个简单运算。
max的微分怎么求
普通的加法、乘法的微分都很好想象,如果这个节点是对输入变量求一个max值呢?此时当前节点对于输入变量的微分分别是多少?
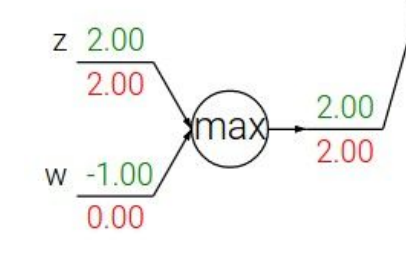
其实也不难想象,答案就是,对于是max的那个变量,微分是1,其它为0。这也非常合理,因为有了这个max的操作,相当于其它变量都对输出不会再产生影响了,那么再把微分传递给它们也用处不大,因为我们关心的是最终的表达式在那些能够影响它的值的那些变量上的微分或者梯度。
Jacobian matrix 雅克比矩阵
因为我们实际上处理的数据大多数是向量化的,那么求导的结果其实是一个雅可比矩阵。不要被这个名字吓到,其实它就是一个用每个输出维度对每个输入维度求导的过程。
假设我们输入的x是n维,输出的y是m维,那么函数f(x) = y 针对x求导得到的雅克比矩阵是m*n的,其i,j位置的值为(d(y_i)/d(x_j))。

(来自维基百科https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant)
主题无关
Serena Yeung的英语听着好舒服,发音很清晰,不拖泥带水,几乎没有不必要的语气词,值得学习~~而且人还很美,感觉这门课的老师们颜值都好高@_@