题目描述
给你一根长度为n的绳子,请把绳子剪成m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
题目分析
首先,将该题目可以建模成:
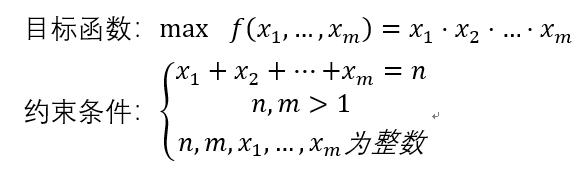
(一)当不考虑未知数是否为整数的情况
可知,首先要找到最佳的m,再找到最佳的m个段长。若m固定的话,怎样将n分配到m段才能让这m段的乘积最大呢?很容易想到,当n均匀分配到m段时,m段长的乘积最大,这也是可以证明得到的。
假设m=2,则x+y=n,f(x,y)=x*y=x*(n-x)=nx-x2,对于这样一个二次函数,它具有最小值n2/4,对应x=y=n/2,这个大家都知道。那么推广到m未知的情况,是怎么样的?
根据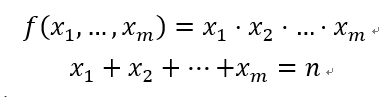
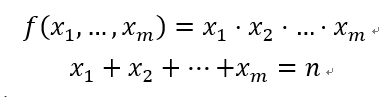
可以消元得到![]()
对函数求偏导并令所有偏导等于0,即可得到极值:
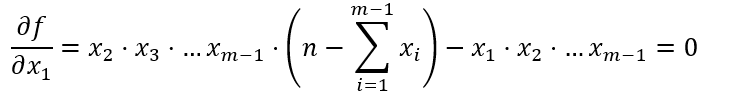 ...
...

化简得到:
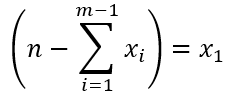
...
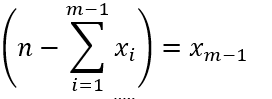
即: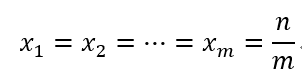
那么可知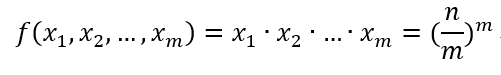
此时f函数在m固定的情况下具有最大值,那么其实m也是个未知数,如何确定m使得f函数最大呢?
我们又可以使用求导令其等于0的方法,不过我们可以稍稍变换一下函数使其更好求导,即函数前加个ln:
![]()
求出了lnf的极值点,那么也就求出了f的极值点: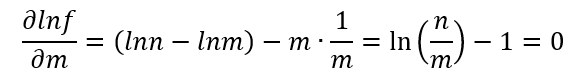
可得: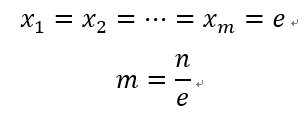
故可知:上式情况下函数f具有最大值
(二)考虑到未知数应为整数的情况
根据我们的建模公式,咱们的未知数都为整数,而在上一步,我们求得的解很可能产生小数,所以我们需要调整。
m的范围最好是在n/e左右,那么就考虑m要么为n/e左边的整数,要么为其右边的整数。
同理,分出来的段长要么为2,要么为3。
python编程实现
1 for i in range(2, 61): 2 m = i/math.e 3 m1 = int(m) if int(m) > 1 else 2 4 m2 = m1 + 1 if int(m) > 1 else 2 5 c1 = int(i/m1) 6 c2 = int(i/m2) 7 r3 = ((c1+1) ** (i - c1 * m1)) * (c1 ** (m1 - i + c1 * m1)) 8 r4 = ((c2+1) ** (i - c2 * m2)) * (c2 ** (m2 - i + c2 * m2)) 9 print(r3 if r3 >= r4 else r4)