关于欧拉函数:
定义:
φ(n)表示1~n中与n互质的数的个数;
求法:
已知n的标准分解式为:
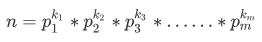 (哦对了,这里所有的因子都是质因子)
(哦对了,这里所有的因子都是质因子)
那么
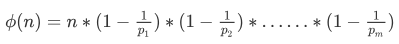
然后求欧拉函数的两种方法:
1.按照定义暴力求解:
int phi(int n){ int ret=n; for(int i=2;i*i<=n;i++){ if(n%i==0){ ret-=ret/i; while(n%i==0) n/=i; } } if(n>1) ret-=ret/n; return ret; }
解释一下:
对于欧拉函数φ来说,我们每*(1-1/pn),就相当于在原数的基础上减掉原数*1/pn(这里的原数并不是指n,而是指n*某些数之后的数),假设原数为ret,那么我们将ret*(1-1/pz)的值就相当于ret-ret*1/pz,由此我们得出了ret-=ret/i;然后将n中的所有i统统除掉,防止出现再算一次的可凉(就是很凉)情况。最后,如果n>1,说明我们还有一个因子没有枚举到,此时n就是当前因子,用上方式子再减一下就好了;
2.欧拉筛时顺带着求出来了???
然后欧拉筛的话,可以求到的值比较小,如果单纯求φ的话,不如用定义呢
#include<iostream> #include<cstdlib> #include<algorithm> #include<ctime> using namespace std; int n,cnt,maxx; int prime[10000010],phi[10000010]; bool not_[10000010]; void shai(){ for(int i=2;i*i<=100000000;i++){ if(!not_[i]) { prime[++cnt]=i; phi[i]=i-1; } for(int j=1;j<=cnt&&i*prime[j]<=n;j++){ not_[i*prime[j]]=1; if(i%prime[j]==0) { phi[i*prime[j]]=phi[i]*prime[j]; break; } else phi[i*prime[j]]=phi[i]*phi[prime[j]]; } } } int main(){ freopen("data.in","r",stdin); freopen("data.ans","w",stdout); cin>>n; shai(); printf("%d",phi[n]); }
end-