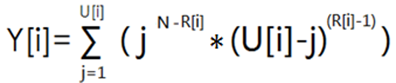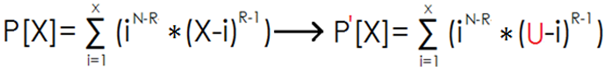题链:
http://www.lydsy.com/JudgeOnline/problem.php?id=4559
题解:
计数dp,拉格朗日插值法。
真的是神题啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊。
先来看看 dp定义:(由于每门课程的分数分布方案是独立的,所以先不管每科实际分数大小所贡献的方案数。)
dp[i][j]:表示前 i门课程,只考虑分数相对大小关系时,B神碾压了 j个人的方法数
也就是说上面的dp定义只是表示一个相对关系的方案数(即不考虑实际分数大小)。
那么dp的转移:
dp[i][k] += dp[i-1][j]*C(j,k)*C(N-j,N-R[i]-k)
含义呢:就是从在前i-1门课程中被碾压的 j 名同学中选出 k 个来继续碾压(即让他们该科分数任比B神低);同时在没有被碾压的 N-j个同学中选出N-R[i]-k个来使得他们的该科分数任比B神低。(使B神排在该门课程的第 R[i]名)
如果设 Y[i]表示第i门课程且B神排在第R[i]名时的分数分布方案数。
则
最后的答案就是 dp[N][k]*Y[1]*Y[2]*Y[3]*...*Y[M]
但是求这个 Y[i]就有点麻烦了,里面的 U[i]很大呀,根本不能跑循环去求和。
然后就要用到插值法了。 (不懂插值法?快点击这里,简单入门一波,很快的 ~)
再明确一下当前的目标: 某一门课程,总分为 U,B神排名为 R,求分数分布方案数。
令函数
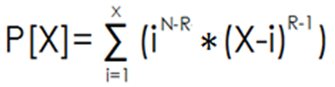
则答案即为 P[U]。
不难发现,求和式的每一项的都不超过 XN-1,同时又最多只有 X项相加,
所以 P[X] 是最高次项的次数不超过 N 的多项式。
那么求出这个多项式,就只需要 N+1个点,就用插值法求出该函数了。
所以O(N2*logN(快速幂的log))的复杂度暴力求出前 N+1个点的函数值
(X1=1,P[1]) , (X2=2,P[2]) ...... (XN+1=N+1,P[N+1])
然后插值法得到函数 P[X]。
然后再 O(N2)的复杂度求出 X=U 时的函数值 P[U],即可得到当前科目的分数分布方案:Y[当前科目]。
又因为有 M 门科目,所以求 Y[]数组的总复杂度为 O(N3*logN)
erge的插值法代码:
ll Lagrange(ll U,ll R)
{
static ll p[MAXN];
for(int i=1;i<=n+1;i++){
p[i]=0;
for(int j=1;j<=i;j++)
p[i]=(p[i]+Pow(j,n-R)*Pow(U-j,R-1))%Mod;
}
ll ret=0;
for(int i=1;i<=n+1;i++){
ll mul=1;
for(int j=1;j<=n+1;j++)if(j!=i)
mul=mul*(U-j+Mod)%Mod*inv[i-j+500]%Mod;
mul=mul*p[i]%Mod;
ret=(ret+mul)%Mod;
}
return (ret+Mod)%Mod;
}
复杂度有点高,但是可以AC。以下是优化。
这里就有一个比较绕的技巧。
因为对于 P[X]来说,不同的 X 取值既影响求和项的个数,又影响每一项的计算参数:
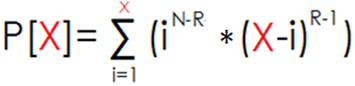
所以我们暴力求前N+1个点的函数值时不得不花费 O(N^2)的代价。
但注意到,我们这么求 P[X]函数是不是太亏了:花费这么高的复杂度却只需要用到 P[U]这一函数值。
所以优化如下,把 P[X] -> P'[X]
注意到了变化么?
是的,我们把求和式的每一项里面的那个自变量 X 改为了一个常数 U。
这样就可以 O(N) 求出前 N+1个点的函数值 P'[X]:
令: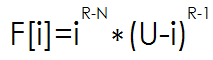
那么 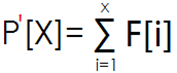
显然是个前缀的形式,即 P'[X]=P'[X-1]+F[i]。(之前的 P[X]可没有这个性质哦)
求出了 P'函数的 N+1个点后,就可以插值法求出 P'[X],并得到 P'[U]的值,返回答案就好了。
(在此,插值法也可以通过一个预处理前后缀积来做到 O(N)计算某一个函数值,这个就自己去看代码的实现了)
等等,不感觉有点不对么?
P'函数有点不对呀,本来 P 函数还是好好的,结果把里面的自变量改变成了常数,怎么P'还是对的?
的确, P'函数几乎是错的。几乎对于所有的自变量 X,P[X]!=P'[X]!
但是有一个 X'是满足 P[X']=P'[X'],那个 X'=U
也就是说 P[U]=P'[U], 这个P'函数只能在 X=U 时得到正确答案。
为什么呢,即我们把 P函数里面的每一项里的自变量 X变成了常数 U 后,
对于 X 取值不为 U时,显然 P[X]!=P'[X]
可是当 X=U 时,就可以把那个已经看成常数U了的自变量X又看回为自变量,即两个函数此时的取值相同了。
换句话说我们构造了另外一个函数P',使得其函数图像与函数P的图像在 X=U时有交点。(我们牺牲了几乎所有的正确性,只保留了最有用的那部分,以此来提高效率。)
吼吼,所以就这样了,求 Y[ ]的复杂度变为了O(N2*logN);
实现看看代码啦。
复杂度 O(N3)(DP部分)+O(N2*logN)(插值法部分)
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 150
#define _ %mod
#define filein(x) freopen(#x".in","r",stdin);
#define fileout(x) freopen(#x".out","w",stdout);
using namespace std;
const int mod=1000000007;
int dp[MAXN][MAXN],U[MAXN],R[MAXN],C[MAXN][MAXN],Y[MAXN],inv[MAXN];
int N,M,K,ANS;
int pow(int a,int b){
int now=1;
while(b){
if(b&1) now=(1ll*now*a)_;
a=(1ll*a*a)_; b>>=1;
}
return now;
}
int Lagrange(int u,int r){
{
/* f(i) = ((i)^(N-R) * (U-i)^(R-1)) //级别最大项为 u^(N-1)
p(x) = ∑|i=1,i<=x| ((i)^(R-N) * (U-i)^(R-1))
= ∑|i=1,i<=x| f(i)
p(x) 级别最大项为 u*u^(N-1)=u^N,所以拉格朗日插值法求其多项式函数需要 N+1 个点
返回的答案为 p(u)。*/
}
static int lpi[MAXN],rpi[MAXN],p[MAXN],ans,tmp;
lpi[0]=1; rpi[N+2]=1; ans=0;
for(int i=1;i<=N+1;i++){
p[i]=(1ll*p[i-1]+1ll*pow(i,N-r)*pow(u-i,r-1)_)_;
if(i==u) return p[i];
}
for(int i=1;i<=N+1;i++) lpi[i]=1ll*lpi[i-1]*(u-i)_;
for(int i=N+1;i>=1;i--) rpi[i]=1ll*rpi[i+1]*(u-i)_;
for(int i=1;tmp=1,i<=N+1;i++){
tmp=1ll*tmp*lpi[i-1]_*rpi[i+1]_*inv[i-1]_*inv[N+1-i]_*p[i]_;
tmp=(1ll*tmp*((N+1-i)&1?-1:1)+mod)_;
ans=(1ll*ans+tmp)_;
}
return ans;
}
int main()
{
scanf("%d%d%d",&N,&M,&K);
inv[0]=1; inv[1]=1;
for(int i=2;i<=N+1;i++) inv[i]=((-1ll*(mod/i)*inv[mod%i])_+mod)_;
for(int i=1;i<=N+1;i++) inv[i]=1ll*inv[i]*inv[i-1]_;
for(int i=1;i<=M;i++) scanf("%d",&U[i]);
for(int i=1;i<=M;i++) scanf("%d",&R[i]);
for(int i=0;i<=N;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(1ll*C[i-1][j-1]+C[i-1][j])_;
}
for(int i=1;i<=M;i++) Y[i]=Lagrange(U[i],R[i]);
dp[0][N-1]=1;
for(int i=1;i<=M;i++)
for(int j=0;j<=N-1;j++)
for(int k=0;k<=min(j,N-R[i]);k++) if(N-1-j>=N-R[i]-k)
dp[i][k]=(1ll*dp[i][k]+1ll*dp[i-1][j]*C[j][k]_*C[N-1-j][N-R[i]-k]_)_;
ANS=dp[M][K];
for(int i=1;i<=M;i++) ANS=1ll*ANS*Y[i]_;
printf("%d",ANS);
return 0;
}