Description
"Hike on a Graph" is a game that is played on a board on which an undirected graph is drawn. The graph is complete and has all loops, i.e. for any two locations there is exactly one arrow between them. The arrows are coloured. There are three players, and each of them has a piece. At the beginning of the game, the three pieces are in fixed locations on the graph. In turn, the players may do a move. A move consists of moving one's own piece along an arrow to a new location on the board. The following constraint is imposed on this: the piece may only be moved along arrows of the same colour as the arrow between the two opponents' pieces.
In the sixties ("make love not war") a one-person variant of the game emerged. In this variant one person moves all the three pieces, not necessarily one after the other, but of course only one at a time. Goal of this game is to get all pieces onto the same location, using as few moves as possible. Find out the smallest number of moves that is necessary to get all three pieces onto the same location, for a given board layout and starting positions.
In the sixties ("make love not war") a one-person variant of the game emerged. In this variant one person moves all the three pieces, not necessarily one after the other, but of course only one at a time. Goal of this game is to get all pieces onto the same location, using as few moves as possible. Find out the smallest number of moves that is necessary to get all three pieces onto the same location, for a given board layout and starting positions.
Input
The input contains several test cases. Each test case starts with the number n. Input is terminated by n=0. Otherwise, 1<=n<=50. Then follow three integers p1, p2, p3 with 1<=pi<=n denoting the starting locations of the game pieces. The colours of the arrows are given next as a m×m matrix of whitespace-separated lower-case letters. The element mij denotes the colour of the arrow between the locations i and j. Since the graph is undirected, you can assume the matrix to be symmetrical.
Output
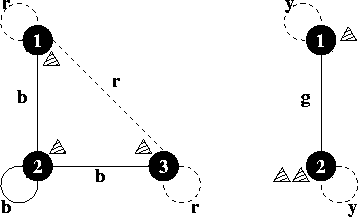 For each test case output on a single line the minimum number of moves required to get all three pieces onto the same location, or the word "impossible" if that is not possible for the given board and starting locations.
For each test case output on a single line the minimum number of moves required to get all three pieces onto the same location, or the word "impossible" if that is not possible for the given board and starting locations.Sample Input
3 1 2 3 r b r b b b r b r 2 1 2 2 y g g y 0
Sample Output
2 impossible
Source
题目大意:有一张图,上面的路径都是着色的,开始的时候有3个盘子在确定的点上,现在让你按要求沿图中的路径移动盘子(一步只能移动一只盘子),问是否能将3个盘子都移到同一个点上,如果可以,输出需要的最少步数,否则输出“impossible”。>_<移动条件是:每个盘子只能沿着这样一条路移动,这条路的颜色和另外的两个盘子之间的路径上标记的颜色是一样的。
解题思路:因为这道题给的是完全图,也就是说图上每两个点之间都有路径存在,它们标记的都有颜色。所以直接BFS就AC啦!
相关链接:过程详解 http://www.cnblogs.com/pcoda/archive/2012/09/02/2667987.html
1 #include<iostream> 2 #include<queue> 3 #include<string> 4 #include<string.h> 5 using namespace std; 6 int n,p1,p2,p3; 7 char map[55][55];//存储图 8 int ans[55][55][55];//保存a[i][j][k]表示3个盘子在i,j,k位置时的最小步数 9 int ok;//记录最终3个盘子的位置,如果为0则imposible 10 struct state{ 11 int a,b,c; 12 }temp;//3个盘子的位置 13 void read(){ 14 cin>>p1>>p2>>p3; 15 for(int i=1;i<=n;i++){ 16 map[i][0]='#';//在这填充个字符,不然就报错 17 for(int j=1;j<=n;j++) 18 cin>>map[i][j]; 19 map[i][n+1]='�';//在行尾加一个结束符,便于后面操作 20 } 21 } 22 void bfs(){ 23 ok=0; 24 fill(&ans[0][0][0],&ans[0][0][0]+55*55*55,255);//将ans初始化很大 25 ans[p1][p2][p3]=0;//令刚开始位置为0(不要少了) 26 queue<state> Q; 27 temp.a=p1;temp.b=p2;temp.c=p3; 28 Q.push(temp); 29 while(!Q.empty()){ 30 state top=Q.front();Q.pop(); 31 int x=top.a,y=top.b,z=top.c; 32 if(x==y && y==z){//如果3盘到一点就跳出 33 ok=x; 34 break; 35 }else{ 36 int cur_ans=ans[x][y][z]; 37 cur_ans++; 38 39 char bc_color=map[y][z]; 40 string str_a=map[x];//(与a连的所有路径) 41 for(int i=1;i<=n;i++){ 42 //遍历所有路径,如果不是自己,且满足移动条件,且ans[i][y][z]>cur_ans就移动 43 if(i!=x && str_a[i]==bc_color && ans[i][y][z]>cur_ans){ 44 ans[i][y][z] = cur_ans; 45 temp.a=i;temp.b=y;temp.c=z; 46 Q.push(temp); 47 } 48 }//a盘的移动 49 50 char ac_color=map[x][z]; 51 string str_b=map[y]; 52 for(int i=1;i<=n;i++){ 53 if(i!=y && str_b[i]==ac_color && ans[x][i][z]>cur_ans){ 54 ans[x][i][z]=cur_ans; 55 temp.a=x;temp.b=i;temp.c=z; 56 Q.push(temp); 57 } 58 }//b盘的移动 59 60 char ab_color=map[x][y]; 61 string str_c=map[z]; 62 for(int i=1;i<=n;i++){ 63 if(i!=z && str_c[i]==ab_color && ans[x][y][i]>cur_ans){ 64 ans[x][y][i]=cur_ans; 65 temp.a=x;temp.b=y;temp.c=i; 66 Q.push(temp); 67 } 68 }//c盘的移动 69 } 70 } 71 } 72 int main(){ 73 while(cin>>n && n){ 74 read(); 75 bfs(); 76 if(ok)cout<<ans[ok][ok][ok]<<' '; 77 else cout<<"impossible "; 78 }return 0; 79 }