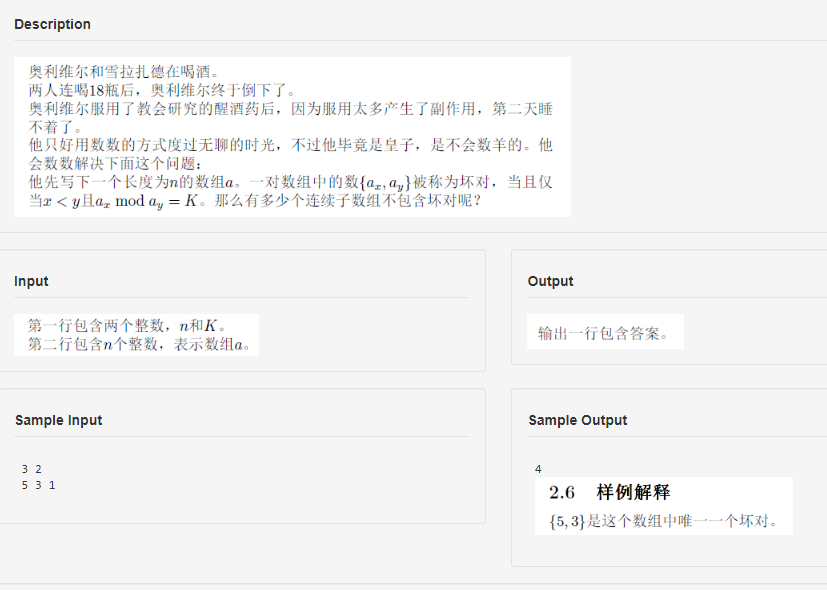
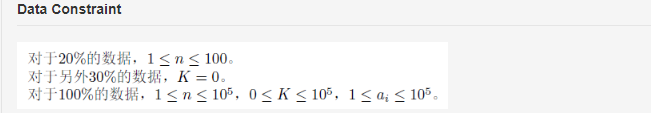
分析:
我遇到这种题真的脑子里只有暴力。。。可是听完解释后才发现并不难。原式子为 $ ax equiv k (mod ay) $,稍微转换一下就是 $ax-k equiv 0 (mod ay)$ 。这就可以转化为ax-k的因数,我们只要利用a数组的大小限制开桶维护最近因数位置即可。但是此题代码实现时我遇到了很多问题。我们先看原式,很显然的ax要大于等于k,ay要大于k。还有终止问题,我们只需记录最接近当前位置的不合法点的位置即可。考虑完这个并把代码实现后却只有50分,在那里百思不得其解。在研究完下来的数据后我发现了一个问题,当ax==k时,任何的ay只要大于k的都不合法,可是我们按ax-k的因数去算,此时0是没有因数的,这时候需要特判一下,血的教训啊。。。对着茫茫数据发了半天呆。
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<queue> 6 #include<algorithm> 7 #include<vector> 8 using namespace std; 9 #define debug printf("zxt ") 10 #define int long long 11 inline int read(){ 12 int a=0,b=1;char c=getchar(); 13 while(!isdigit(c)){if(c=='-')b=-1;c=getchar();} 14 while(isdigit(c)){a=a*10+c-'0';c=getchar();} 15 return a*b; 16 } 17 const int N=5e6+50; 18 int n,k,m,a[N],tot,t[N],ans,rem,zxt; 19 signed main(){ 20 freopen("drink.in","r",stdin); 21 freopen("drink.out","w",stdout); 22 n=read();k=read(); 23 tot=n; 24 for(int i=1;i<=n;i++){ 25 a[tot--]=read(); 26 } 27 int maxn=0; 28 for(int i=1;i<=n;i++){ 29 if(a[i]<k){ 30 ans+=i-zxt; 31 } 32 else{ 33 m=a[i]-k; 34 rem=0; 35 if(m){ 36 for(int j=1;j*j<=m;j++){ 37 if(m%j==0){ 38 if(j>k)rem=max(rem,t[j]); 39 if(m/j>k) rem=max(rem,t[m/j]); 40 } 41 } 42 } 43 else{ 44 for(int j=k+1;j<=maxn;j++) 45 if(t[j])rem=max(rem,t[j]); 46 } 47 zxt=max(zxt,rem); 48 ans+=i-zxt; 49 } 50 t[a[i]]=i; 51 maxn=max(maxn,a[i]); 52 } 53 printf("%lld ",ans); 54 return 0; 55 }