1.动态规划解决0-1背包问题
0-1背包问题:给定n种物品和一个背包.物品i的种类为wi,价值为vi,背包容量为C.问:应该如何选择装入背包的物品,使得装入背包中物品的总价值最大?
其中每种物品只有两种选择,即装入背包和不装入背包.
##首先找到最优子结构

##然后找到递归关系

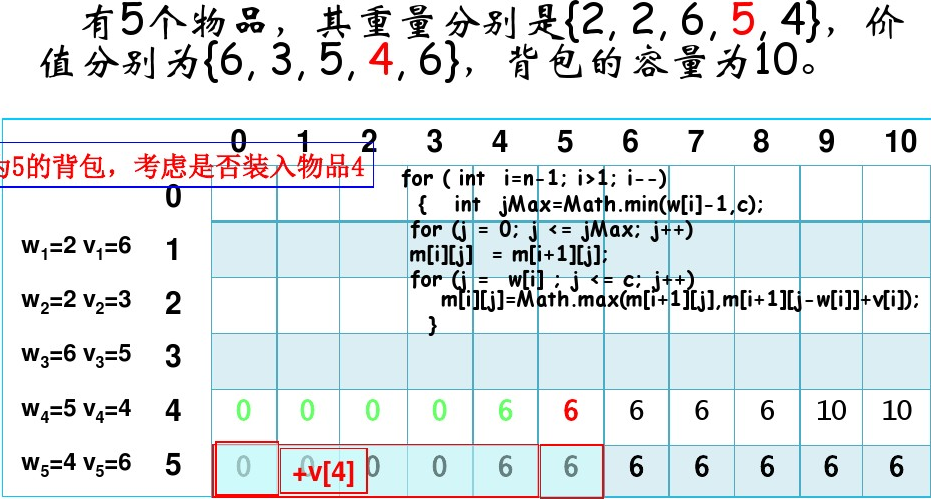
##算法描述在下
通过递归,将所有的结果值保存在一个矩阵中

/** * 动态规划0-1背包算法 * @author 邹龄晋 * 答案:15 11001 */ public class Demo { public static void main(String[] args) { int [] w = {2,2,6,5,4};//对应重量 int [] v = {6,3,5,4,6};//对应价值 int c = 10;//总质量 int [][] m = new int[v.length][c+1];//定义m二维数组用来表示所有的价值,m[i][j]表示第i物品装入容量为j的背包的最大值 int [] x = new int[w.length]; //解空间集 Knapsack(v,w,c,m); traceback(m,w,c,x); System.out.println("m[0][c]="+m[0][c]); for(int i=0;i<x.length;i++){ System.out.print(x[i]+" "); } System.out.println(); for(int i=0;i<v.length;i++){ for(int j=0;j<c+1;j++){ System.out.print(m[i][j]+" "); } System.out.println(); } } public static void traceback(int [][]m,int []w,int c,int []x){ int n = w.length-1; for(int i=0;i<n;i++) if(m[i][c]==m[i+1][c]) x[i] = 0; else{ x[i] = 1; c-=w[i]; } x[n] = (m[n][c]>0)?1:0; } public static void Knapsack(int v[],int w[],int c,int [][]m){ int n = v.length-1; int jMax = Math.min(w[n]-1, c); for(int j=0;j<=jMax;j++) m[n][j] = 0; for(int j=w[n];j<=c;j++) m[n][j] = v[n]; for(int i=n-1;i>=0;i--){ jMax = Math.min(w[i]-1, c); for(int j=0;j<=jMax;j++) m[i][j] = m[i+1][j]; for(int j=w[i];j<=c;j++) m[i][j] = Math.max(m[i+1][j],m[i+1][j-w[i]]+v[i]); } } }

m[0][c]=15 1 1 0 0 1 0 0 6 6 9 9 12 12 15 15 15 0 0 3 3 6 6 9 9 9 10 11 0 0 0 0 6 6 6 6 6 10 11 0 0 0 0 6 6 6 6 6 10 10 0 0 0 0 6 6 6 6 6 6 6
看完程序后我们看下面两个图帮助理解