求迷宫从入口到出口的所有路径是一个经典的程序设计问题,求解迷宫,通常采用的是“穷举+回溯”的思想,即从入口开始,顺着某一个方向出发,若能够走通,就继续往前走;若不能走通,则退回原路,换一个方向继续向前探索,直到所有的通路都探寻为止。因此本文依据这种“穷举+回溯”的思想,设计一个求解迷宫的程序。
1 问题分析
为了保证在任何位置上都能够退回原路,显然需要使用一个先进后出的数据结构来保存已经探寻过的位置,因此在程序求解迷宫路径的过程中采用栈这种数据结构。
迷宫是一个二维地图,其中含有出口和入口,障碍点和通道,因此程序采用一个二位数组map来表示,其中,二维数组值所代表的含义如下:
0:通道 1:起点 2:障碍 3:终点 4:路径需要注意的是,最后求解出来的通路,必须要是一条简单路径,即在求得的路径上不能重复出现同一通道快。下面简述一下程序的求解过程。
将“在搜索过程中某一个时刻所在迷宫地图中的位置“记为“当前位置”,那么求解迷宫路径算法的基本思想是:若“当前位置”可通行,那么将“当前位置”纳入求解路径中(压到栈中),并朝“下一个位置”继续探索,即把“下一位置”切换到“当前位置”,如此重复下去,直到找到出口;如果当前位置不可以通行,则顺着来的方向退回到“前一个通道位置”,然后再朝着其他方向探索下去;如果该通道块的4个方向(东西南北)都不可通,那么就在该路径(栈)中删除该通道位置(删除栈顶元素),再继续退回到“前一个通道位置”继续探索,即再获取栈顶元素作为“当前位置继续上述的重复探索。
2 算法描述
根据对迷宫问题的分析,求迷宫中一条从入口到出口的路径算法描述如下:
-
设定入口位置为当前位置。
-
if(当前位置是可通行且是没有被走过的通道块 )
(分支1)2.1 将当前位置压到栈中。
2.2 若当前位置是出口,
则程序结束,返回路径栈。2.3 若当前不是出口,则切换当前位置为当前位置东边的通道块,
返回2继续执行。 -
else(若当前位置不可通行)
(分支2)3.1 获取栈顶元素所在的位置,若该位置所在的相邻4个方向都被探索过了,则删除当前栈顶元素,获取新的栈顶元素,直到找到一个可通的相邻块位置或出栈至栈空
再执行3.2步骤。3.2 若栈顶元素所在的位置还有其他方向没有被探索过,则设定新的当前位置为栈顶元素的未被探索方向的相邻通道块。(方向访问顺序为顺时针即东南西北)
-
重复步骤2.
需要注意步骤2中的没有被走过的通道块,是指该通道块从来未压入栈中,否则求解的路径就不是一条简单路径,很可能导致一个死循环。
3 程序实现
程序采用c#语言对上述的算法描述进行了实现,代码如下。
3.1 通到块实体
class PathElement
{
public PathElement(int row, int col, int direcation)
{
this.Row = row;
this.Col = col;
this.Direction = direcation;
}
public int Row;//位置所在的行
public int Col;//位置所在的列
public int Direction;//从此位置走向下一位置的方向,方向分为东0南1西2北3,默认东方向为初始方向
}3.2 寻找简单路径
public static Stack<PathElement> FindPath(int[,] map, int startX, int startY, int endX, int endY)
{
Stack<PathElement> path = new Stack<PathElement>();
List<PathElement> visitedList = new List<PathElement>();//保存以通过的元素
PathElement curPosition = new PathElement(startX, startY, 0);
int tryCount = 0;
do
{
tryCount++;
if (Pass(curPosition, map) && (!Visited(curPosition, visitedList)))//当前位置能通过,且没被访问过
{
path.Push(curPosition);//加入路径
if (curPosition.Row == endX && curPosition.Col == endY)
return path;
visitedList.Add(curPosition);//该位置以被访问
curPosition = GetNextPosition(curPosition);//获取下一个当前位置,并更新该位置的下一个位置的方向
}
else//当前不能通过
{
if (path.Count != 0) //如何栈不为空
{
PathElement topElement = path.Peek();//获取栈顶元素
while (topElement.Direction == 4 && (path.Count > 1))//找寻一个可用的位置
{
path.Pop();
topElement = path.Peek();
}
if (topElement.Direction < 4)
{
curPosition = GetNextPosition(topElement);//获取下一个当前位置,并更新该位置的下一个位置的方向
}
}
}
} while (path.Count != 0);
return null;
}3.3 辅助方法
/*获取下一个位置*/
private static PathElement GetNextPosition(PathElement curPostion)
{
PathElement nextPosition=null;
switch (curPostion.Direction)
{
case 0:
nextPosition = new PathElement(curPostion.Row, curPostion.Col+1, 0);
break;
case 1:
nextPosition = new PathElement(curPostion.Row+1, curPostion.Col, 0);
break;
case 2:
nextPosition = new PathElement(curPostion.Row, curPostion.Col-1, 0);
break;
case 3:
nextPosition = new PathElement(curPostion.Row-1, curPostion.Col, 0);
break;
}
curPostion.Direction++;
return nextPosition;
}
/*是否为通道*/
private static bool Pass(PathElement curPosition, int[,] map)
{
int rowCount = map.GetLength(0);
int colCount = map.GetLength(1);
//边界判断
if (curPosition.Row >= 0 && curPosition.Row < rowCount && curPosition.Col >= 0 && curPosition.Col < colCount)
{
//障碍判断
if (map[curPosition.Row, curPosition.Col] == 2)
{
return false;
}
else
{
return true;
}
}
else
{
return false;
}
}
/*是否被访问*/
private static bool Visited(PathElement curPosition, List<PathElement> visitedList)
{
foreach (PathElement element in visitedList)
{
if (element.Row == curPosition.Row && element.Col == curPosition.Col)
{
return true;
}
}
return false;
}3.4 界面
该部分代码只是提供算法验证的可视化界面,与本文所探讨的算法实现没有多大的关系,程序的源代码可以在文章后面的链接进行下载。
界面所包含的功能:
- 能够编辑迷宫地图,单击实现障碍物的设计,双击去掉障碍物。
- 能够保存和载入地图。
- 能够通过该算法实现从迷宫入口到出口路径的生成和显示。
3.5 结果截图
1 地图的载入

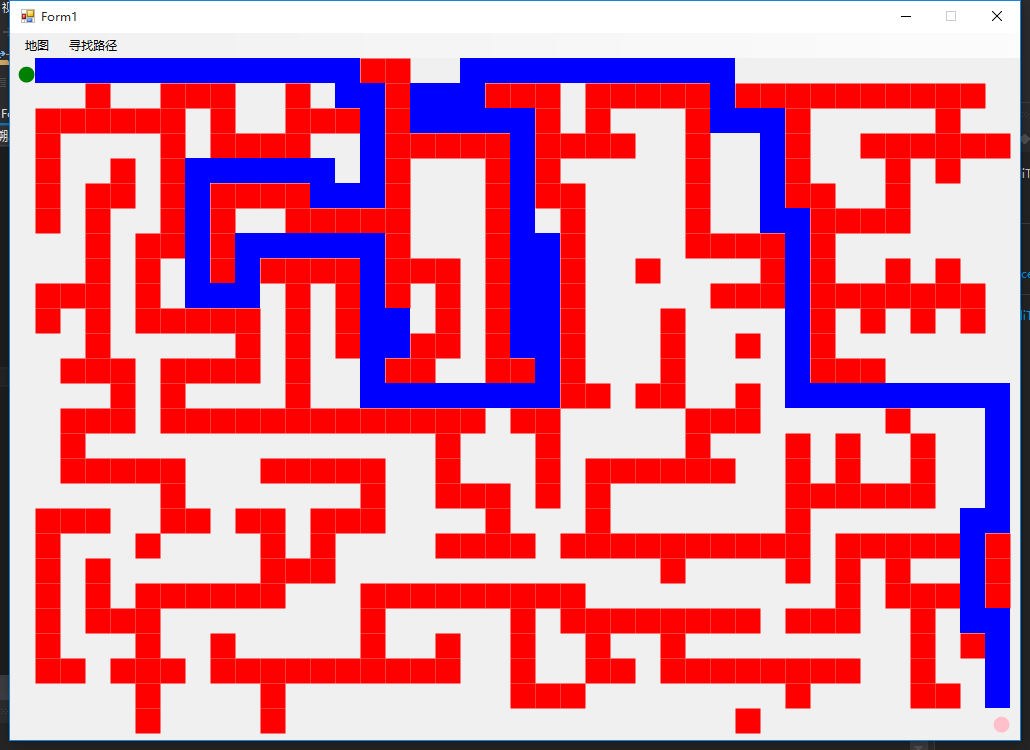
2 路径寻找
4 总结
“穷举+回溯”的思路还是很好理解,通俗的讲,就是选择一条道路一直走到黑,如果碰到前方有障碍,就退回来一步再换一个方向继续走,直到把所有可能的路都做完了。
利用“穷举+回溯”搜索路径,虽然简单,但是它属于一种盲目、机械的搜索算法,从3.5中的结果图中可以看出,该算法找出来的路径,显然不是最优的,走了许多的弯路。那么如何从迷宫的起点到终点找到一条最优的路径呢?敬请期待《迷宫问题求解之“A*搜索”(二)》。
5 资源和参考资料
参考资料:严蔚敏《数据结构c语言版》