蓝桥学院2019算法题2.6

汉诺塔题目要求：

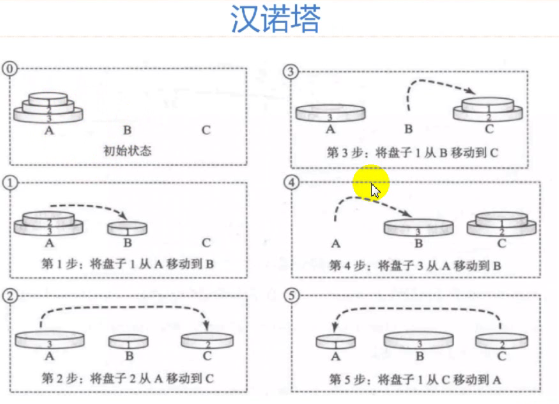
解题思路：

1~N从A移动到B，C作为辅助

　　等价于：

　　1、1~N-1从A移动到C，B作为辅助

　　2、把N从A移动到B

　　3、1~N-1从C移动到B，A为辅助

算法实现：

package recursion;

/**
 * @author zsh
 * @company wlgzs
 * @create 2019-02-16 8:53
 * @Describe 汉诺塔
 */
public class TowerOfHanoi {

    /**
     *  将N个盘子从原始柱子移动到目标柱子的路径打印
     * @param N 初始的盘子大小，N为最大编号
     * @param from 原始柱子
     * @param to 目标柱子
     * @param help 辅助柱子
     * 解题思路：
     * 找重复：1到N-1个盘子移动到辅助空间，N移动到目标柱子。
     * 找变化量：N
     * 找出口：N == 1
     */
    static void printHanoiTower(int N,String from,String to,String help){
        if (N == 1){
            System.out.println("move" + N +from+"to"+to);
            return;
        }
        //先把N-1个盘子挪到辅助空间上去
        printHanoiTower(N -1 ,from,help,to);
        //N可以顺利到达目标柱子
        System.out.println("move" + N +from+"to"+to);
        //让N-1个盘子回到源空间上去
        printHanoiTower(N-1,help,to,from);
    }

    public static void main(String[] args) {
        printHanoiTower(3,"A","B","C");
    }
}