一、四种平均算法
- 平方平均数:Qn=√ [(a12+a22+...+an2)/n] ——>应用:标准差
- 算术平均数:An=(a1+a2+...+an)/n ——>1阶平均 ,是加权算数平均的一种特殊形式,缺点:容易受极端值影响
- 几何平均数:Gn=(a1·a2...an)1/n ——>
- 调和平均数:Hn=n/(1/a1+1/a2+...+1/an) ——>-1阶平均 ——>调和平均给予较小值更高的权重
关系满足:调和平均Hn ≤ 几何平均Gn ≤ 算数平均An ≤ 平方平均Qn
加权算术平均、加权几何平均、算数-几何平均等都是 基于以上4种进一步得来。
拓展1——>若有两个正实数 x 和 y,那么其算数平均数列{an},几何平均{bn}都会收敛,并收敛至同一实数,这个数称为 x 和 y 的算术-几何平均数,记为 M(x, y) 或 agm(x, y)。
拓展2——>加权算数平均
拓展3——>移动平均
原理:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。
应用:当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。
拓展4——>加权调和平均 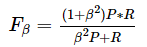 ,
,
β>1:召回率(Recall)影响更大,eg. F2
β<1:查准率(Precision)影响更大,eg. F0.5
β=1:得到 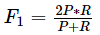 ,即 F1 score。
,即 F1 score。
二、F1 score
F1 score是一个平均数,选择了最后一种调和平均数算法进行计算,对精确率P与召回率R 进行平均的一个结果;
公式: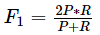
几何意义:图中的直线和各个机器学习PR曲线的交点表示recall和precision的一个“平衡点”,它是另外一种度量方式,即定义F1值
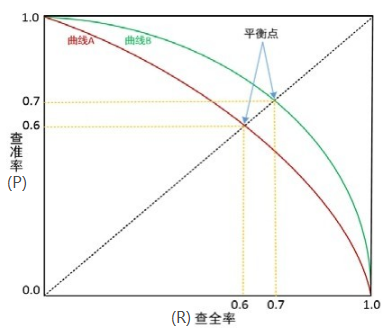
特点:就是会更多聚焦在较低的值,所以会对每个指标非常重视;
看harmony公式变形:Hn=2*a*b/(a+b);a+b恒等于1,a*b=a*(1-a)=-a^2+a; 令导数为-2a+1=0,a=0.5时值最大;Hn的最大值为0.5,从这里可以看出如果a+b有约束的情况下,a与b的值越接近Hn值越大;
在F1 sore这里,a与b不存在共同约束,只有0<=a<=1,0<=b<=1,所以最大值不只只是0.5。比如说Hn=2*1*1/(1+1)=1,这也是最完美的,此时,精确率与召回率都是100%;
【参考】
β<1:查准率(Precision)影响更大,eg. F0.5
拓展4——>加权调和平均 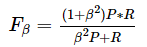 ,
,
β>1:召回率(Recall)影响更大,eg. F2
β<1:查准率(Precision)影响更大,eg. F0.5
β=1:得到 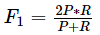 ,即 F1 score
,即 F1 score