Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.
A k-tree is an infinite rooted tree where:
- each vertex has exactly k children;
- each edge has some weight;
- if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, ..., k.
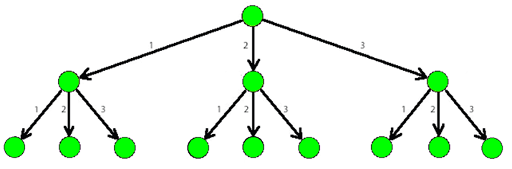
The picture below shows a part of a 3-tree.
Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 (109 + 7).
A single line contains three space-separated integers: n, k and d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k).
Print a single integer — the answer to the problem modulo 1000000007 (109 + 7).
3 3 2
3
3 3 3
1
4 3 2
6
4 5 2
7
题目描述
最近有一个富有创造力的学生Lesha听了一个关于树的讲座。在听完讲座之后,Lesha受到了启发,并且他有一个关于k-tree(k叉树)的想法。 k-tree都是无根树,并且满足:
- 每一个非叶子节点都有k个孩子节点;
- 每一条边都有一个边权;
- 每一个非叶子节点指向其k个孩子节点的k条边的权值分别为1,2,3,...,k。
当Lesha的好朋友Dima看到这种树时,Dima马上想到了一个问题:“有多少条从k-tree的根节点出发的路上的边权之和等于n,并且经过的这些边中至少有一条边的边权大于等于d呢?” 现在你需要帮助Dima解决这个问题。考虑到路径总数可能会非常大,所以只需输出路径总数 mod 1000000007 即可。(1000000007=10^9+7)
考虑dp[ i ][ 1/0 ]表示总和为i时,最大值是否>=d的方案数;
然后枚举中间状态转移;
注意long long ;
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 1000005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
ll qpow(ll a, ll b, ll c) {
ll ans = 1;
a = a % c;
while (b) {
if (b % 2)ans = ans * a%c;
b /= 2; a = a * a%c;
}
return ans;
}
/*
int n, m;
int st, ed;
struct node {
int u, v, nxt, w;
}edge[maxn<<1];
int head[maxn], cnt;
void addedge(int u, int v, int w) {
edge[cnt].u = u; edge[cnt].v = v; edge[cnt].w = w;
edge[cnt].nxt = head[u]; head[u] = cnt++;
}
int rk[maxn];
int bfs() {
queue<int>q;
ms(rk);
rk[st] = 1; q.push(st);
while (!q.empty()) {
int tmp = q.front(); q.pop();
for (int i = head[tmp]; i != -1; i = edge[i].nxt) {
int to = edge[i].v;
if (rk[to] || edge[i].w <= 0)continue;
rk[to] = rk[tmp] + 1; q.push(to);
}
}
return rk[ed];
}
int dfs(int u, int flow) {
if (u == ed)return flow;
int add = 0;
for (int i = head[u]; i != -1 && add < flow; i = edge[i].nxt) {
int v = edge[i].v;
if (rk[v] != rk[u] + 1 || !edge[i].w)continue;
int tmpadd = dfs(v, min(edge[i].w, flow - add));
if (!tmpadd) { rk[v] = -1; continue; }
edge[i].w -= tmpadd; edge[i ^ 1].w += tmpadd; add += tmpadd;
}
return add;
}
ll ans;
void dinic() {
while (bfs())ans += dfs(st, inf);
}
*/
int n, k, d;
ll dp[200][2];
int main()
{
//ios::sync_with_stdio(0);
//memset(head, -1, sizeof(head));
while (cin >> n >> k >> d) {
ms(dp); dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= k; j++) {
if (i >= j) {
if (j < d) {
dp[i][0] = (dp[i][0] + dp[i - j][0]) % mod;
dp[i][1] = (dp[i][1] + dp[i - j][1]) % mod;
}
else {
dp[i][1] = (dp[i][1] + dp[i - j][0] + dp[i - j][1]) % mod;
}
}
}
}
cout << (ll)dp[n][1] << endl;
}
return 0;
}