调和级数:1/1+2/1+3/1+...+1/n=log(n);
(准备好暴力了吗~~~)
1:[1,n]中k的倍数有多少个?
ans:(下取整)n/k;
2:[1,n]中每个数的约数有多少个?
for(int i=1;i<=n;i++)
for(int j=1;i*j<=n;j++)
ans[i*j]++;
调和级数原理:时间复杂度:O(log(n));
3:判断质数:
bool is_prim(int x)
{
if(x==1)return false;
for(int i=2;i*i<=x;i++)
if(x%i==0)return false;
return true;
}
两数互质:记作:a⊥b
4:
π(n)为不超过n的质数个数;
π(n)≈n/ln(n);
5:埃筛(nloglogn筛素数)
#include<bits/stdc++.h>
using namespace std;
int n,m;
bool isprim[10000005];
int endp;
int ls;
int main(){
scanf("%d%d",&n,&m);
memset(isprim,1,sizeof(isprim));
endp=sqrt(n);
isprim[1]=false;
for(int i=1;i<=endp;i++){
if(isprim[i])
for(int j=2;j*i<=n;j++)
isprim[j*i]=false;
}
for(int i=1;i<=m;i++){
scanf("%d",&ls);
if(isprim[ls])
printf("Yes
");
else
printf("No
");
}
return 0;
}
6:质因数分解
每一个数都可以唯一的分解成n个质数的k次方相乘的形式
int p[N]
int fenjie(int x)
{
int cnt=0;
for(int i=2;i*i<=x;i++){
while(x%i==0){
p[++cnt]=i;
x/=i;
}
}
if(x>1)p[++cnt]=x;
}
分解质因数后两数的乘除可转化成指数加减的形式
同时也可以用指数相减是否大于等于0判断一数能否整除另一数
一个数的因子数等于所有质因子的指数加一相乘后的结果(π)
7:随时取模
a=a/p(下取整)*p+a%p;
在只含加法减法和乘法的式子里如果最后的结果要对p取模,可以在式子里随便取模;
取模的最后结果可能出现负数:转化:((ans%p)+p)%p变为最小正值
每一个数都可以写成:a1*1+a2*10+a3*100。。。。的形式,由此可得出模数为三时a1+a2+a3。。。。%3=0即可得出原式%3=0
同样的只需a1*1+a2*10%4=0,即可得出原式%4=0;
8:gcd and lcm;
1:可用质因数分解求解(一般不用)
gcd(a,b)=gcd(b,a%b);
求解gcd:
void gcd(int a,int b)
{
if(b==0)return a;
return gcd(b,a%b);
}
求解lcm:
void lcm(int a,int b)
{
return a/gcd(a,b)*b;
}
9:逆元
如果在%p的情况下除a和乘b所得结果相同,我们称a为b的逆元或b为a的逆元
inv(a)为a的逆元
inv(x)*x≡1(%p)
inv(a*b)=inv(a)*inv(b);
费马小定理:
若p为质数:
n^(p-1)≡1(%p)
n为任意正整数
so:
inv(x)*x≡x^(p-1)(%p)
两边同时除以x:
inv(x)≡x^(p-2)(%p)
只有a,b互质时a才在%b下存在逆元
裴蜀定理:
关于整数x,y的不定方程
ax+by=gcd(a,b)
必定有解
so:
我们知道
bx+(a%b)y=gcd(a,b)
求解
ax1+by1=gcd(a,b)
(x1,y1)=(y,x-a/b(下取整)*y)
扩展欧几里得(手推)
int x,y;
int ls;
void exgcd(int a,int b)
{
if(b==0){
x=1;
y=0;
return ;
}
exgcd(b,a%b);
ls=x;
x=y;
y=ls-a/b*y;
}
a即为%b意义下的逆元
来了来了!!!!
线性递推求模质数逆元:
inv[1]=1;
for(int i=2;i<p;i++)
inv[i]=(p-p/i)*inv[p%i]%p;
(p为质数,代码可求出在模p意义下1~p-1中所有数的逆元)
9.5:阶乘逆元
求组和数:
定义:fac[x]表示(x!)%p;
{
fac[0]=1;
for(int i=1;i<p;i++)
fac[i]=fac[i-1]*i%p;
}
inv[x]表示x!在模p意义下的逆元
{
1:利用线性递推求模质数的逆元
inv[0]=inv[1]=1;
for(int i=2;i<p;i++)
inv[i]=(p-p/i)*inv[p%i]%p;
for(int i=1;i<p;i++)
inv[i]=inv[i-1]*inv[i]%p;
2:exgcd求解
利用exgcd求解n!的逆元
然后利用inv[n-1]=inv[n]*n;
递推求解
}
so:c(m,n)=fac[n]*inv[m]%p*inv[n-m]%p;
10:线性同余方程
中国剩余定理(CRT)
x≡a1(%m1)
x≡a2(%m2)
x≡a3(%m3)
……
x≡an(%mn)
ans%(M)=∑(i=1;i<=n;i++)ai*inv mi (Mi)*Mi ;: (Mi=a1*a2*a3*…*an/ai),M(m1*m2*m3*…*mn);
ans有无数个,每M个中有一个满足条件
11:排列组合;
为什么不看看数学书呢?
组合数: 公式递推代码 C(n, m) = C(n -1, m - 1) + C(n - 1, m) (pascal公式)
模意义下:lucas定理:c(n,m)=c(n/p,m/p)*c(n%p,m%p)%p;(p为质数):log(n)求解
c(0,0)=1;
12:杂项
有个类似分治的办法算快速幂和快速乘(为什么不看看书呢?)
现在有n个正整数,需要从中取出k个数,使得他们的gcd最大,求这个gcd;
从大到小枚举,在输入时记录n[x],当n[gcd]+n[2*gcd]+n[3*gcd]+…+n[n*gcd]>=k时满足条件
由于调和级数,最后的时间复杂度为nlog(n);
可能想不起来:
(1):不等式;
(2):1+2+3+…+n=n*(n+1)/2;
1^2+2^2+3^2+…+n^2=n*(n+1)*(2*n+1)/6;
1^3+2^3+3^3+…+n^3=[n(n+1)/2]^2
13:欧拉函数:
φ(x):小于x的与x互质的正整数的个数
φ(x)=x*π(连乘符号)(1-1/p);(p为x的质因子)
若a⊥b那么φ(a*b)=φ(a)*φ(b);
线性筛素数andφ:
https://www.cnblogs.com/grubbyskyer/p/3852421.html
欧拉定理:
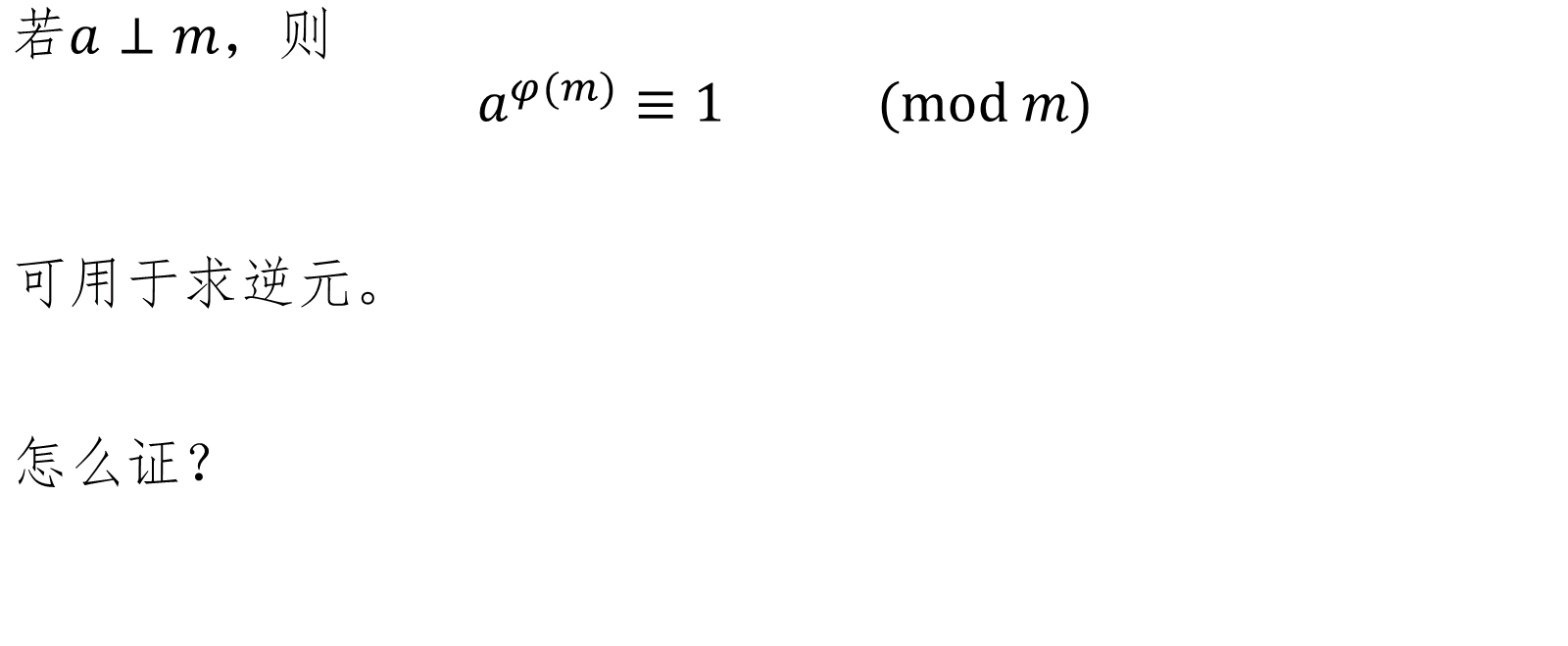
哼唧,不证