https://nanti.jisuanke.com/t/77
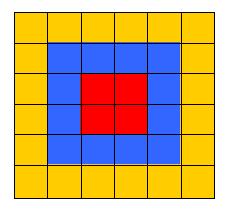
晓萌这几天使劲的往一个n 行n列的矩阵填0和1这两个数字,n为偶数,而且矩阵由里向外分成了n / 2层。比如n = 6时,矩阵的分层如下:
晓萌填数时有一个要求:不能存在位于不同层的两个相邻的1(这里的相邻指两格子共用一条线)。
请你帮晓萌计算一下有多少种填法。
输入包含多组测试数据,每组数据包含一个偶数n (2 ≤ n ≤ 500)。
请计算并输出对2012取余后的结果。
提示
当n = 4时
1011 0100 0100 0000
是满足要求的
1111 0100 0100 0000
是不满足要求的,因为第一行第二列的1和第二行第二列的1相邻且位于不同的层。
样例输入
2 4
样例输出
16 1952
可以把图分为四块互不相关的部分,以下图为例
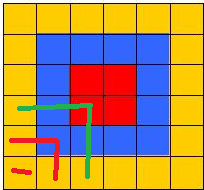
按照图中的线把图形拉直可以发现每一条线都是互不相关的,
而且可以看出满足条件的是不能有连续的1出现,
找出规律后发现是斐波那契数列。
接下来就是算这一小块总的可能填法,为f[1] * f[3] * f[5] * ...... * f[n-1]。
上面算的只是四分之一,而事故部分又是互不相关的,所以四块的可能数是一样的。
所以答案为上面算出的一块的4次方。
#include<stdio.h>
#define N 550
long long a[N];
int main()
{
int i,n;
long long sum;
a[0]=1;
a[1]=2;
for(i=2;i<=520;i++)
a[i]=(a[i-1]+a[i-2])%2012;
while(scanf("%d",&n)!=EOF)
{
sum=1;
for(i=1;i<=n/2;i++)
sum=(sum*a[2*i-1])%2012;
printf("%lld
",(sum*sum*sum*sum)%2012);
}
return 0;
}