单调栈
定义:
单调栈,顾名思义,是栈内元素保持一定单调性(单调递增或单调递减)的栈。这里的单调递增或递减是指的从栈顶到栈底单调递增或递减。既然是栈,就满足后进先出的特点。与之相对应的是单调队列。
实现:
先上结论:
利用单调栈,可以找到从左/右遍历第一个比它小/大的元素的位置
一:
举个例子:
假设有一个单调递增的栈 S和一组数列:
a : 5 3 7 4
用数组L[i] 表示 第i个数向左遍历的第一个比它小的元素的位置
如何求L[i]?
首先我们考虑一个朴素的算法,可以按顺序枚举每一个数,然后再依此向左遍历。
但是当数列单调递减时,复杂度是严格的O(n^2)。
此时我们便可以利用单调栈在O(n)的复杂度下实现
我们按顺序遍历数组,然后构造一个单调递增栈
(1). i = 1时,因栈为空,L[1] = 0,此时再将第一个元素的位置下标1存入栈中
此时栈中情况:

(2).i = 2时,因当前3小于栈顶元素对应的元素5,故将5弹出栈
此时栈为空
故L[2] = 0
然后将元素3对应的位置下标2存入栈中
此时栈中情况:

(3).i = 3时,因当前7大于栈顶元素对应的元素3,故
L[3] = S.top() = 2 (栈顶元素的值)
然后将元素7对应的下标3存入栈
此时栈中情况:
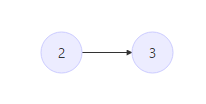
(4).i = 4时,为保持单调递增的性质,应将栈顶元素3弹出
此时 L[4] = S.top() = 2;
然后将元素4对应的下标3存入栈
此时栈中情况:
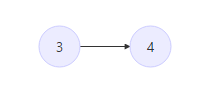
至此 算法结束
对应的结果:
a : 5 3 7 4
L : 0 0 2 2
二:
例如实现一个单调递增的栈,比如现在有一组数10,3,7,4,12。从左到右依次入栈,则如果栈为空或入栈元素值小于栈顶元素值,则入栈;否则,如果入栈则会破坏栈的单调性,则需要把比入栈元素小的元素全部出栈。单调递减的栈反之。
10入栈时,栈为空,直接入栈,栈内元素为10。
3入栈时,栈顶元素10比3大,则入栈,栈内元素为10,3。
7入栈时,栈顶元素3比7小,则栈顶元素出栈,此时栈顶元素为10,比7大,则7入栈,栈内元素为10,7。
4入栈时,栈顶元素7比4大,则入栈,栈内元素为10,7,4。
12入栈时,栈顶元素4比12小,4出栈,此时栈顶元素为7,仍比12小,栈顶元素7继续出栈,此时栈顶元素为10,仍比12小,10出栈,此时栈为空,12入栈,栈内元素为12。
至于代码的实现我觉得还是必须对应着题目去体会,也没有太死板的模板,下面只给出伪代码吧。
/*
* 本伪代码对应的是单调递减栈
*共n个元素,编号为0~n-1
*/
while(栈为空) 栈顶元素出栈; //先清空栈
a[n]=-1;
for(i=0;i<=n;i++)
{
if(栈为空或入栈元素大于等于栈顶元素) 入栈;
else
{
while(栈非空并且栈顶元素大于等于入栈元素)
{
栈顶元素出栈;
更新结果;
}
将最后一次出栈的栈顶元素(即当前元素可以拓展到的位置)入栈;
更新最后一次出栈的栈顶元素其对应的值;
}
}
输出结果;
将破坏栈单调性的元素都出栈后,最后一次出栈的元素就是当前入栈元素能拓展到的最左位置,更新其对应的值,并将其位置入栈。(注: 对于这句话到现在都没有理解, 如果有大佬路过可以帮我解释解释。)
应用:
以上就是一个单调栈的定义及其实现,下面就来说一下它可以解决哪些问题。其实我也不能给出证明,以证明它为什么能完成这些功能,只是简单的把它的用途说一下,碰到问题时就需要大家灵活运用了。
1.最基础的应用就是给定一组数,针对每个数,寻找它和它右边第一个比它大的数之间有多少个数。
2.给定一序列,寻找某一子序列,使得子序列中的最小值乘以子序列的长度最大。
3.给定一序列,寻找某一子序列,使得子序列中的最小值乘以子序列所有元素和最大。
对应题目:做的还不多,以后慢慢增加。
1、完美矩阵;
这题选拔赛做的时候没有写出来,主要因为太菜, 想到用单调栈,但没有考虑的很全面,先说说我看到的第一感觉,用贪心,在每一层以高度递增遍历每一层,问题出在当时找到连续的就break了,没有继续往后找,不过以数据大小来说这样写一定会TLE的,之后想到单调栈,但以高度入栈了,写的一团乱。直到学长讲解的时候思路才打开,应该以下标入栈。分别在左右找他的第一个小于他的数。就A了。这个实现不难就不贴下来了。后面再网上看到了两个写法,思路大致相同不过各有优劣。
-找出每一个单位宽度矩形的左边界 l 和右边界 r ,左边界定义为左边连续的高度大于等于它的最左边的矩形的下标,右边界同理,从左往右推出所有的左边界,从右往左推出所有的右边界。
注意:矩形的高度h可以等于零,以为这当左边边上的矩形高为零或者右边边界上矩形高度为零时,while循环无法停止,所以在while循环的条件中要加上限制边界的条件。
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define max(a, b) ((a > b) ? (a) : (b))
long long h[100010],l[100010],r[100010];
int main()
{
int n;
scanf("%d",&n);
int i, t;
for(i=1; i<=n; i++)
{
scanf("%lld",&h[i]);
}
memset(l, 0, sizeof(l));
memset(r, 0, sizeof(r));
l[1]=1;
r[n]=n;
for(i=2; i<=n; i++)
{
t=i;
while(t>1&&h[i]<=h[t-1])
t=l[t-1];
l[i]=t;
}
for(i=n-1; i>0; i--)
{
t=i;
while(t<n&&h[i]<=h[t+1])
t=r[t+1];
r[i]=t;
}
long long s=0;
for(i=1; i<=n; i++)
{
s = max(s, (r[i]-l[i]+1)*h[i]);
}
printf("%lld
",s);
return 0;
}
- 利用根据单调递增栈解决,如果栈为空或入栈元素小于栈顶元素则入栈,否则会破坏栈的单调性,则将栈顶元素出栈并更新结果,直到栈为空或碰到一个小于入栈元素的值。然后将当前元素入栈。这个方法还没有彻底掌握,先贴代码。
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<stack>
using namespace std;
typedef long long LL;
int main()
{
int i,n,top; //top指向栈顶
stack<int> st; //栈用于保存矩形的编号,即位置
LL tmp,ans,a[100010]; //tmp为临时变量,记录面积的值,ans为结果,记录最大面积值
while(~scanf("%d",&n)&&n)
{
for(i=0;i<n;i++)
scanf("%lld",&a[i]);
ans=0;
a[n]=-1; //最后一个元素设为最小值,以最后清空栈
for(i=0;i<=n;i++)
{
if(st.empty()||a[i]>=a[st.top()])
{ //如果栈为空或入栈元素大于等于栈顶元素 ,则入栈
st.push(i);
}
else
{
while(!st.empty()&&a[i]<a[st.top()])
{ //如果栈非空且入栈元素小于栈顶元素,则将栈顶元素出栈
top=st.top();
st.pop();
tmp=(i-top)*a[top]; //在出栈过程中计算面积值
if(tmp>ans) ans=tmp; //更新面积最大值
}
st.push(top); //只将可以延伸到的最左端的位置入栈
a[top]=a[i]; //并修改该位置的值
}
}
printf("%lld
",ans);
}
return 0;
}