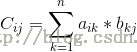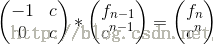矩阵快速幂

（1）矩阵乘法

简单的说矩阵就是二维数组，数存在里面，矩阵乘法的规则:A*B=C

其中c[i][j]为A的第i行与B的第j列对应乘积的和，即:

另外，矩阵也可以用一个结构体来表示

struct matrix
{
    ll a[N][N];
};

矩阵乘法代码实现：

matrix mul(matrix x,matrix y)
{
    matrix temp;
    for(int i = 1 ; i < N ; i++)
        for(int j = 1 ; j < N ; j++)
        temp.a[i][j] = 0;
    for(int i = 1 ; i < N ; i++)
        for(int j = 1 ; j < N ; j++)
                for(int k = 1 ; k < N ; k++)
                    temp.a[i][j] += x.a[i][k]*y.a[k][j];
    return temp;
}

这个实现代码复杂度是O(n^3)的，其实还有更低复杂度的算法实现。利用分块矩阵即可，比较复杂。。不多说了。

(2)矩阵快速幂

类似于整数的快速幂，把整数快速幂中的整数换成矩阵、乘法换成矩阵乘法就可以了。

代码实现：

matrix quickpow(matrix a,long long n)
{
    matrix res;
    res.a[1][1] = 1; res.a[1][2] = 0; res.a[1][3] = 0;
    res.a[2][1] = 0; res.a[2][2] = 1; res.a[2][3] = 0;
    res.a[3][1] = 0; res.a[3][2] = 0; res.a[3][3] = 1;//初始化为单位矩阵
    while(n)
    {
        if(n&1) res = mul(res,a);//判断n是否为奇数
        a = mul(a,a);
        n>>=1;//二分
    }
    return res;
}

(3)应用

通过改变转移矩阵的值，将普通递推式改写成矩阵形式。然后用快速幂求解最终矩阵。

给一道简单例题：poj 3070 http://poj.org/problem?id=3070

题目：斐波那契数列f(n),给一个n，求f(n)%10000,n<=1e9;（本题是可以用递推完成的，且可以用记忆化数组的方法加速递推，这里略去不做解释）

解法：先列出Fibonacci递推式: f(1) = 1.f(2) = 2. f(n) = f(n-1) + f(n-2)  (n > 2) 

接下来建立矩阵形式的递推，找到转移矩阵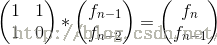，记作T*A(n-1) = A(n).（可以推出1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);）

得出最终矩阵A(n) = T^n-1*A(1),这里的A(1)成为初始矩阵，接下来利用矩阵快速幂就可以得到res，res[1][1]=f(n)就是我们要求的。

给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

2.f(n)=c^n-f(n-1) ；（c是常数）