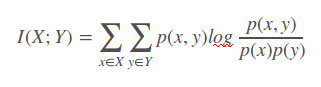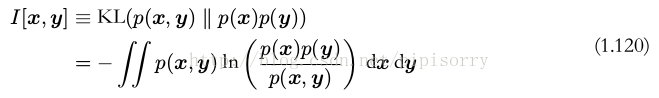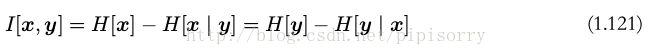一、概念
互信息,Mutual Information,缩写为MI,表示两个变量X与Y是否有关系,以及关系的强弱,或者说是X与Y的相关性。
如果 (X, Y) ~ p(x, y), X, Y 之间的互信息 I(X; Y)定义为:
Note: 互信息 I (X; Y)可为正、负或0。
互信息实际上是更广泛的相对熵的特殊情形
如果变量不是独立的,那么我们可以通过考察联合概率分布与边缘概率分布乘积之间的 Kullback-Leibler 散度来判断它们是否“接近”于相互独立。此时, Kullback-Leibler 散度为
这被称为变量 x 和变量 y 之间的互信息( mutual information )。根据 Kullback-Leibler 散度的性质,我们看到 I[x, y] ≥ 0 ,当且仅当 x 和 y 相互独立时等号成立。
使用概率的加和规则和乘积规则,我们看到互信息和条件熵之间的关系为
可以把互信息看成由于知道 y 值而造成的 x 的不确定性的减小(反之亦然)(即Y的值透露了多少关于X 的信息量)。


Y的熵指的是衡量的是Y的不确定度,Y分布得越离散,H(Y)的值越高
H(Y|X)则表示在已知X的情况下,Y的不确定度
所以,根据互信息公式的变形:
可以看出,I(X,Y)可以解释为由X引入而使Y的不确定度减小的量,这个减小的量为H(Y|X)
所以,如果X,Y关系越密切,I(X,Y)就越大
I(X,Y)最大的取值是H(Y),此时H(Y|X)为0,意义为X和Y完全相关,在X确定的情况下Y是个定值,没有出现其他不确定情况的概率,所以为H(Y|X)为0
I(X,Y)取0时,代表X与Y独立,此时H(Y)=H(Y|X),意义为X的出现不影响Y
二、性质
I(X;Y)的性质:
1)I(X;Y)⩾0
2)I(X;Y)= H(X)−H(X|Y) = I(Y;X)=H(Y)−H(Y|X):这里我们可以得到:当X和Y完全相关时,互信息的取值是H(X),同时H(X)=H(Y);当二者完全无关时,互信息的取值是0
3)当X,Y独立时,I(X;Y)=0,
4)当X,Y知道一个就能推断另一个时,I(X;Y)=H(X)=H(Y)
三、互信息、条件熵与联合熵的区别与联系

由于 H(X|X) = 0, 所以, H(X) = H(X) – H(X|X) = I(X; X)
这一方面说明了为什么熵又称自信息,另一方面说明了两个完全相互依赖的变量之间的互信息并不是一个常量,而是取决于它们的熵。
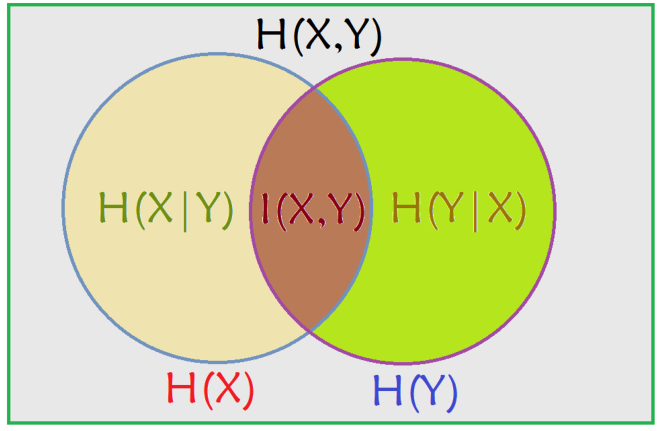
从图中可以看出,条件熵可以通过联合熵 - 熵( H(X|Y) = H(X, Y) - H(Y) )表示,也可以通过熵 - 互信息( H(X|Y) = H(X) - I(X; Y) )表示。
决策树中的信息增益就是互信息,决策树是采用的上面第二种计算方法,即把分类的不同结果看成不同随机事件Y,然后把当前选择的特征看成X,则信息增益就是当前Y的信息熵减去已知X情况下的信息熵。
通过下图的刻画更为直观一些
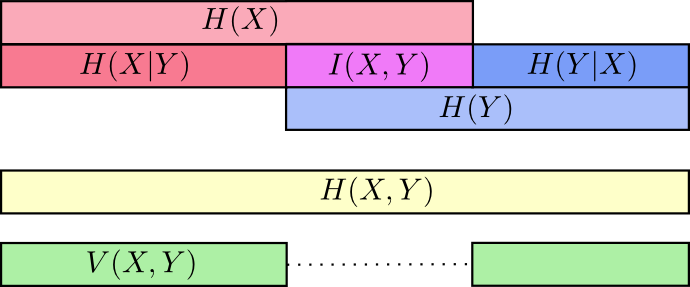
以上图可以清楚的看到互信息I(X,Y)I(X,Y)的不同求法
参考:
https://blog.csdn.net/qq_15111861/article/details/80724278
https://www.cnblogs.com/gatherstars/p/6004075.html
https://blog.csdn.net/haolexiao/article/details/70142571