妙

n个点的树，每个点有一个点权，求包含1号的联通块中点权和前k小的是多少，不足k个则全部输出。

前置技能：k短路 http://blog.csdn.net/wyfcyx_forever/article/details/45875055

我们以1为根建树，考虑一个包含1的联通块，就相当于割掉了某些通向叶子节点的边。

我们把一条边的边权当做深度比较深的那个断点的子树点权和，把每个叶子节点和t连通，我们就是要求s-t的k大割（因为是在总点权里面减掉这些割）。

树是一棵平面图，所以可以转化为对偶图k长路，对于每条边两边两块连一条该边边权的边就行了。

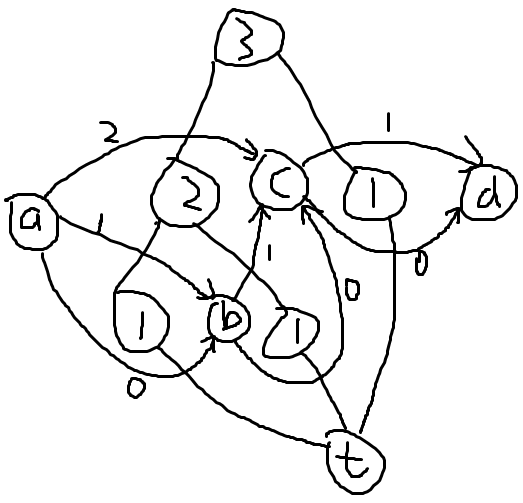
大致如上图，顶点内的数字是子树大小，无向边是树边，abcd是对偶图顶点，有向边是对偶图的。

你问我好不好写？无可奉告。

（而且这题k短路预处理还卡spfa，必须写bfs）

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc 
int M=0,fst[SZ],vb[SZ],nxt[SZ];ll vc[SZ];
void ad_de(int a,int b,ll c)
{++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}
void adde(int a,int b,ll c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{
"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;
",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{
"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;
",i,vb[e]); puts("}");}
#define SZ 666666
int n,k,v[SZ];
ll tot;
namespace ng //ng...
{
int n,s,t; Edgc
ll dist[SZ];
ll gd(int x)
{
    if(dist[x]!=dist[0]) return dist[x];
    ll minn=1e18;
    for esb(x,e,b) minn=min(minn,gd(b)+vc[e]);
    return dist[x]=minn;
}
#define K 131071
void spfa(int S)
{
    memset(dist,127/3,sizeof(dist)); dist[S]=0;
    for(int i=1;i<=n;i++) gd(i);
}
//lajixiaohuoche
//huiwoqingchun
struct node {node *l,*r;ll v;int t,d;node(){d=0;l=r=0;}}
pool[1234567],*P=pool,*rs[SZ];
node* alc(ll v,int t)
{
    node* g=P++;
    g->v=v; g->t=t;
    return g;
}
inline int gd(node* s) {return s?s->d:0;}
node* mg(node* a,node* b)
{
    if(!a&&!b) return 0;
    node *tg=P++;
    if(!a||!b)
    {
        if(!a) *tg=*b;
        else *tg=*a;
        return tg;
    }
    if(a->v>b->v) swap(a,b);
    *tg=*a; tg->r=mg(tg->r,b);
    if(gd(tg->l)<gd(tg->r)) swap(tg->l,tg->r);
    tg->d=gd(tg->r)+1;
    return tg;
}
int fa[SZ];
vector<int> ch[SZ];
bool te[SZ];
int qs[SZ];
typedef pair<ll,node*> rec;
priority_queue<rec,vector<rec>,greater<rec> >pq;
void pushq()
{
    int h=0,t=0; qs[t++]=n;
    while(h^t)
    {
        int x=qs[h++];
        rs[x]=mg(0,rs[fa[x]]);
        for esb(x,e,b) if(!te[e])
        {
            ll cb=vc[e]-(dist[x]-dist[b]);
            rs[x]=mg(rs[x],alc(cb,b));
        }
        for(int i=ch[x].size()-1;i>=0;i--)
        qs[t++]=ch[x][i];
    }
}
void pre()
{
    spfa(n);
    for(int i=1;i<n;i++)
    {
        for esb(i,e,b)
        {
            ll c=vc[e];
            if(dist[i]==dist[b]+c)
            {
                fa[i]=b; te[e]=1;
                ch[b].pb(i); break;
            }
        }
    }
    pushq();
    vector<ll> anss;
    anss.pb(dist[1]);
    pq.push(rec(dist[1]+rs[1]->v,rs[1]));
    for(int i=1;i<k&&!pq.empty();i++)
    {
        rec g=pq.top(); pq.pop(); anss.pb(g.fi);
        if(rs[g.se->t]) pq.push(rec(g.fi+rs[g.se->t]->v,rs[g.se->t]));
        if(g.se->l) pq.push(rec(g.fi-g.se->v+g.se->l->v,g.se->l));
        if(g.se->r) pq.push(rec(g.fi-g.se->v+g.se->r->v,g.se->r));
    }
    for(int i=0;i<k&&i<anss.size();i++) printf("%lld
",tot+anss[i]);
}
}
namespace ot
{
Edg
int fa[SZ],dep[SZ];
ll sz[SZ];
int leaf[SZ],ln=0;
void dfs(int x,int f=0)
{
    sz[x]=v[x]; bool l=1;
    for esb(x,e,b) if(b!=f)
        fa[b]=x, dep[b]=dep[x]+1, dfs(b,x),
        sz[x]+=sz[b], l=0;
    if(l) leaf[++ln]=x;
}
int col[SZ];
//route from a--lca(a,b) has painted
void paint(int a,int b,int t)
{
    while(a!=b)
    {
        if(dep[a]<dep[b])
            col[b]=t, b=fa[b];
        else
        {
            ng::ad_de(col[a],t,-sz[a]);
            a=fa[a];
        }
    }
}
void pall()
{
    paint(1,leaf[1],++ng::n);
    for(int i=2;i<=ln;i++)
    paint(leaf[i-1],leaf[i],++ng::n);
    paint(leaf[ln],1,++ng::n);
    for(int i=1;i<ng::n;i++)
    ng::ad_de(i,i+1,0);
    ng::s=1; ng::t=ng::n;
}
}
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d",v+i);
    for(int i=1;i<n;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        ot::adde(a,b);
    }
    ot::dfs(1); ot::pall();
    tot=ot::sz[1]; ng::pre();
}