题目大意:自己看去...
题解:做了一下午...本蒟蒻立志要写全网最详细的题解。╭(╯^╰)╮
begin....
暴力70分。可以让空格子到处乱走,只要某个状态的指定格子到目标格子,那么此时的
步数就是最小的啦。
ps:一开始我写的bfs...写到一半不会记录状态..后来看题解,只需要记录空格子和指定棋子
的位置就可以啦。其他的棋子都不变。暴力代码后面会给出。
时间复杂度呢就是q次询问,加上空格子和指定格子的位置就是O(q(nm)^2)。
正解呢..emmm...组织一下语言...orz...
我们发现我们只在一张图上进行q次询问..每次都进行bfs,那也太浪费时间了 。
而且,贪心的想,要想让指定棋子到目标位置,一定要让空格子到指定棋子周围吧。所以在一堆
指定棋子和空格子的状态中,只有空格子在指定棋子四周的状态是有用的。所以我们把这些状态
给抽离出来。
有用状态:空格子在指定棋子的上下左右。
有用状态的后继状态:
(1)本来空格子在指定棋子上下左右的状态的后继可以是空格子还是在棋子的上下左右,
也就是空格子围着指定格子转。
这个步数用bfs计算。
(2)本来空格子在指定棋子上下左右的后继状态是空格子与指定棋子交换了位置。步数为1。
记录状态:我们知道了这些状态怎么记录呢?
就是给棋盘重新标号。不是n*m的棋盘从第一行到最后一行1.2.3.4.5...。而是对状态进行标号。
对于某个棋子,假设到它的标号为k,那么假设它为指定棋子的位置,当空格子在它上面时,这个
状态为k+1,下面时k+2..左边k+3,右边k+4,再下一个棋子,当空格子在它上面时k+5,下面时k+6..
先理解标号是怎样的,后面再详细讲怎样标号。
让状态连续:上面的事情干完我们得到的只是,如果当前格子是指定格子,空格子在它的上/下/左/右/
然后去它上/下/左/右的步数或空格子与它交换的步数。但是这些状态是不连续的。所以我们要用边把它连起来。
就形成图啦。你就会得到下面这么一坨东西。
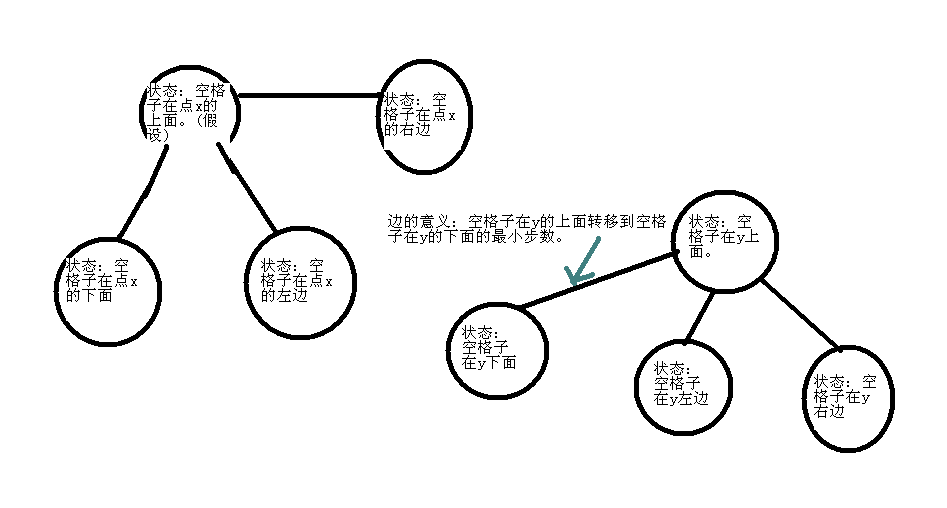
当然这张图还没画完,不是之前说状态不连续么?我还没有画上空格子和指定棋子交换位置的线呢。
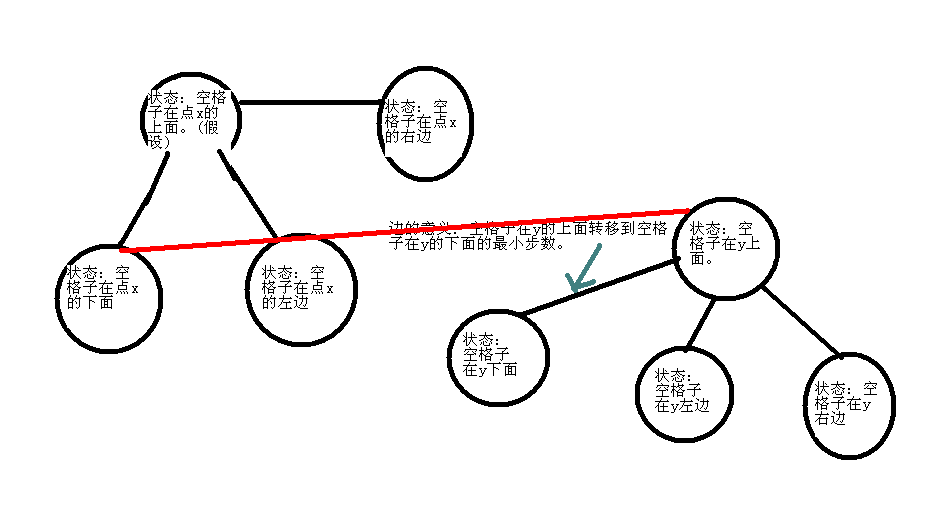
然后图就连通了...
然后跑spfa求最短路径...
只是还有一个问题,终点一定在图上了,但是起点可能与图隔绝。
首先终点状态是什么,就是空格子在tx,ty四周。所以一定在图上。
但是可能起点sx,sy周围没有空格子,所以先让空白格到指定格周围,然后我们就求出
空白格到指定格周围的最小步数,还是bfs。
好。现在理一下思路。
由于只有当空白格在指定格周围状态才有用,我们要抽离出有用状态。
对于指定棋子可能待得地方都抽离状态并计算出后继状态。0,1,2,3,表示空白格到指定格的方向,下面详细讲。
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(map[i][j]){ if(map[i-1][j])bfs(i-1,j,i,j,0); if(map[i][j+1])bfs(i,j+1,i,j,1); if(map[i+1][j])bfs(i+1,j,i,j,2); if(map[i][j-1])bfs(i,j-1,i,j,3); }
标号 0 1 2 3表示空格子在指定棋子的上右下左,这样方便给状态标号。
而且在写mx[4]={...},my[4]={...}也要对应上右下左。
也方便连接空格子和指定格子交换位置时的边,看下面代码。
构图。目的是让状态连续,让状态称为点,边权为状态转移的步数,就是上面的图上连的边。
pre_dis[x][y]表示空格子到(x,y)的最小步数。
void bfs(int ex,int ey,int sx,int sy,int d){ memset(pre_dis,-1,sizeof(pre_dis)); pre_dis[ex][ey]=0;pre_dis[sx][sy]=1; Node now,nxt;now.x=ex;now.y=ey; while(!q.empty())q.pop(); q.push(now); while(!q.empty()){ now=q.front();q.pop(); int x=now.x,y=now.y; for(int i=0;i<4;i++){ int xx=x+mx[i],yy=y+my[i]; if(xx<1||xx>n||yy<1||yy>m||!map[xx][yy]||pre_dis[xx][yy]!=-1)continue; pre_dis[xx][yy]=pre_dis[x][y]+1; nxt.x=xx;nxt.y=yy; q.push(nxt); } } if(d==4)return; int id=get_id(sx,sy); for(int i=0;i<4;i++) if(pre_dis[sx+mx[i]][sy+my[i]]>0) add(id+d,id+i,pre_dis[sx+mx[i]][sy+my[i]]); add(id+d,get_id(ex,ey)+(d+2)%4,1); //这是让空格和指定格交换0123标号的妙处 }
spfa最短路 起点可能不在图中,再跑bfs连边。
最后的目标状态就是指定棋子在tx,ty,然后枚举空格子在tx,ty的上下左右求最小。
代码:
瞎bfs

#include<iostream> #include<cstdio> #include<queue> #include<cstring> using namespace std; int ans,n,m,qx,tx,ty; int t[40][40],vis[40][40][40][40]; int mx[4]={0,1,0,-1}, my[4]={-1,0,1,0}; struct Node{ int ex,ey,sx,sy,ste; }now; queue<Node>q; void read(int &x){ char ch=getchar();x=0;int f=1; for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; for(;isdigit(ch);ch=getchar())x=x*10+ch-'0'; x=x*f; } void BFS(){ memset(vis,0,sizeof(vis)); Node tmp,cur; vis[now.sx][now.sy][now.ex][now.ey]=true; while(!q.empty())q.pop();q.push(now); while(!q.empty()){ cur=q.front();q.pop(); if(cur.sx==tx&&cur.sy==ty){ ans=cur.ste; return; } for(int i=0;i<4;i++){ tmp=cur; int xx=tmp.ex+mx[i],yy=tmp.ey+my[i]; if(!t[xx][yy]||xx<1||xx>n||yy<1||yy>m)continue; if(xx==tmp.sx&&yy==tmp.sy)tmp.sx=tmp.ex,tmp.sy=tmp.ey; tmp.ex=xx;tmp.ey=yy;tmp.ste=cur.ste+1; if(!vis[tmp.sx][tmp.sy][tmp.ex][tmp.ey]){ vis[tmp.sx][tmp.sy][tmp.ex][tmp.ey]=true; q.push(tmp); } } } } int main(){ read(n);read(m);read(qx); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) read(t[i][j]); for(;qx;qx--){ read(now.ex);read(now.ey);read(now.sx);read(now.sy);read(tx);read(ty); now.ste=0;ans=n*m; BFS(); if(ans!=n*m)printf("%d ",ans); else printf("-1 "); } return 0; }
正解

#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; #define maxn 5000 #define inf 2147483647 int n,m,qx,sumedge,ans,ex,ey,sx,sy,tx,ty,p; int map[40][40],pre_dis[40][40],head[maxn],vis[maxn],dis[maxn]; int mx[4]={-1,0,1,0}, my[4]={0,1,0,-1}; struct Node{ int x,y; }cur,nxt; queue<Node>q; queue<int>qn; struct Edge{ int x,y,z,nxt; Edge(int x=0,int y=0,int z=0,int nxt=0): x(x),y(y),z(z),nxt(nxt){} }edge[maxn]; void add(int x,int y,int z){ edge[++sumedge]=Edge(x,y,z,head[x]); head[x]=sumedge; } int get_id(int i,int j){ return (i-1)*m*4+(j-1)*4; } void bfs(int ex,int ey,int sx,int sy,int d){ memset(pre_dis,-1,sizeof(pre_dis)); pre_dis[ex][ey]=0;pre_dis[sx][sy]=1; Node now,nxt;now.x=ex;now.y=ey; while(!q.empty())q.pop(); q.push(now); while(!q.empty()){ now=q.front();q.pop(); int x=now.x,y=now.y; for(int i=0;i<4;i++){ int xx=x+mx[i],yy=y+my[i]; if(xx<1||xx>n||yy<1||yy>m||!map[xx][yy]||pre_dis[xx][yy]!=-1)continue; pre_dis[xx][yy]=pre_dis[x][y]+1; nxt.x=xx;nxt.y=yy; q.push(nxt); } } if(d==4)return; int id=get_id(sx,sy); for(int i=0;i<4;i++) if(pre_dis[sx+mx[i]][sy+my[i]]>0) add(id+d,id+i,pre_dis[sx+mx[i]][sy+my[i]]); add(id+d,get_id(ex,ey)+(d+2)%4,1); } void spfa(int sx,int sy){ memset(dis,-1,sizeof(dis)); memset(vis,0,sizeof(vis)); while(!qn.empty())qn.pop(); int id=get_id(sx,sy); for(int i=0;i<4;i++) if(pre_dis[sx+mx[i]][sy+my[i]]!=-1){ dis[id+i]=pre_dis[sx+mx[i]][sy+my[i]]; qn.push(id+i); } while(!qn.empty()){ int cur=qn.front();qn.pop();vis[cur]=false; for(int i=head[cur];i;i=edge[i].nxt){ int v=edge[i].y; if(dis[v]>dis[cur]+edge[i].z||dis[v]==-1){ dis[v]=dis[cur]+edge[i].z; if(!vis[v]){ vis[v]=true; qn.push(v); } } } } } int main(){ scanf("%d%d%d",&n,&m,&qx); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&map[i][j]); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(map[i][j]){ if(map[i-1][j])bfs(i-1,j,i,j,0); if(map[i][j+1])bfs(i,j+1,i,j,1); if(map[i+1][j])bfs(i+1,j,i,j,2); if(map[i][j-1])bfs(i,j-1,i,j,3); } for(int i=1;i<=qx;i++){ scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty); if(sx==tx&&sy==ty){ printf("0 "); continue; } bfs(ex,ey,sx,sy,4); ans=inf; spfa(sx,sy); int id=get_id(tx,ty); for(int j=0;j<4;j++) if(dis[id+j]!=-1)ans=min(ans,dis[id+j]); if(ans==inf) ans=-1; printf("%d ",ans); } return 0; }
