Capacity of MIMO Channel
we consider the evaluation of the channel capacity of a frequency nonselective
AWGN MIMO channel characterized by the channel matric H. Let s denote
the Ny x 1 transmitted signal vector whose elements are statistically stationary with
zero mean and covariance matrix Rss In the presence of AWGN, the NR x 1 received
signal vector is expressed as
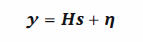
where n is the NR x 1 zero mean Gaussian noise vector with covariance matrix NolNR,
where lNR is the NR x NR identity matrix. Although the channel matrix H is a realization
of a random matrix, in this section we treat H as deterministic and known to the
receiver.


where tr(Rss) denotes the trace of the signal covariance Rss. This(C) is the maximum rate
per Hz that can be transmitted reliably (without errors) over the MIMO channel for any
given realization of the channel matrix H.

Capacity of SIMO Channel
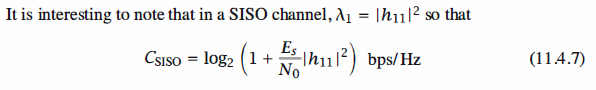
It is can be seen that the capacity of the MIMO channel is simply equal to the sum of the
capacities of r SISO channels, where the transmit energy per SISO channel is Es/ NT
and the corresponding channel gain is equal to the eigenvalue /| i.
Capacity of SIMO Channel

Capacity of MISO Channel

It is interesting to note that for the same ll h ll2, the capacity of the SIMO channel
is greater than the capacity of the MISO channel when the channel is known to the
receiver only. The reason is that, under the constraint that the total transmitted energy
in the two systems be identical, the energy Es in the MISO system is split evenly among
the NT transmit antennas, whereas in the SIMO system, the transmitter energy Es is
used by the single antenna. Note also that in both SIMO and MISO channels, the
capacity grows logarithmically as a function of II h ll 2.
Matlab coding
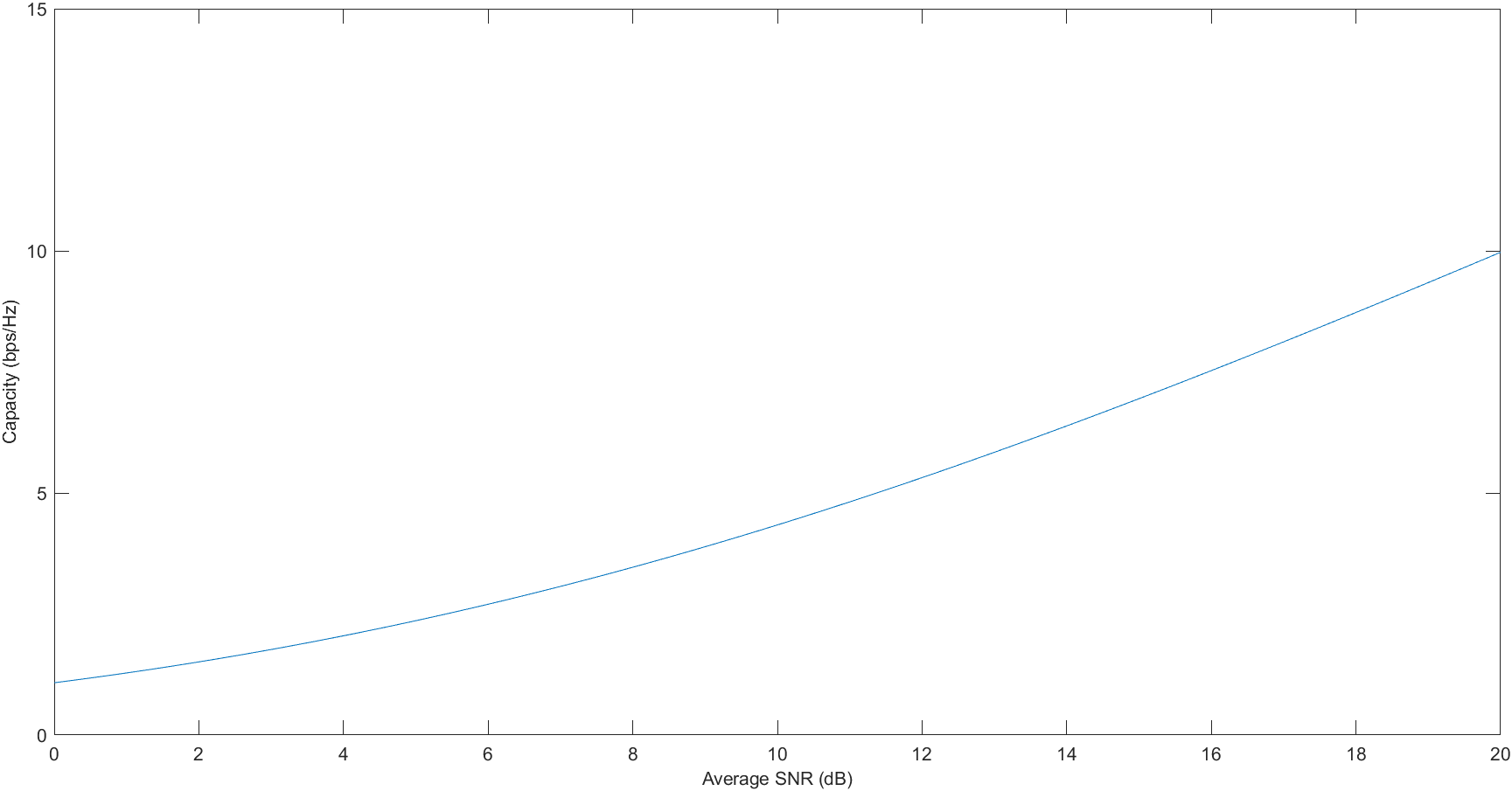
1 % MATLAB script for capacity of MIMO channels 2 Nt = 2; % No. of transmit antennas 3 H = [1 0.5; 0.4 0.8]; % Channel realization 4 lamda = eig(H*H'); % Eigenvalue calculation 5 SNR_dB = 0:0.01:20; % SNR in dB 6 SNR = power(10,SNR_dB/10); 7 % Capacity calculation: 8 C = log2(1 + SNR*lamda(1)/Nt) + log2(1 + SNR*lamda(2)/Nt); 9 disp(['The eigenvales are: ', num2str(lamda')]); 10 % Plot the results: 11 plot(SNR_dB,C) 12 axis([0 20 0 15]) 13 xlabel('Average SNR (dB)','fontsize',10) 14 ylabel('Capacity (bps/Hz)','fontsize',10)
Simulation Result
1 % MATLAB script of capacity of SIMO and MISO channels 2 echo on; 3 H_simo = [1 0.5]'; % Channel realization 4 H_miso = [1 0.5]; % Channel realization 5 Nt_miso = 2; % No. of transmit antennas 6 Nr_simo = 2; % No. of receive antennas 7 SNR_dB = 0:0.01:20; % SNR in dB 8 SNR = power(10,SNR_dB/10); 9 % Capacity calculations: 10 C_simo = log2(1 + SNR*sum(H_simo.^2)); 11 C_miso = log2(1 + SNR*sum(H_miso.^2)/Nt_miso); 12 % Plot the results: 13 plot(SNR_dB,C_simo,'-.',SNR_dB,C_miso) 14 axis([0 20 0 15]) 15 xlabel('Average SNR (dB)','fontsize',10) 16 ylabel('Capacity (bps/Hz)','fontsize',10) 17 legend('SIMO','MISO')
Simulation Result
Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis