Markov Weight Fields for Face Sketch Synthesis
相关知识点:马尔可夫随机场(MRF)
1. Introduction
画像合成方法:MRF(Markov Random Fields)
缺点:
- 不能合成新的sketch patches,因为它是从training sketch patches 选出最好的一个sketch patch,因此并不能很好地表达出目标图片的特征,尤其是对于眼睛、嘴巴和其他细节。
- 优化问题为NP-hard,BP(Belief Propagation)算法也不能保证得到最优解。
提出方法:
- MWF(Markov Weight Fields),在MRF的基础上,不是选出一个代表性sketch patch,而是利用training sketch patches 合成一个新的sketch patch。而且,可以将问题转化为convex Quadratic Programming(凸二次优化问题,QP问题),使其可解。
- CDM(Cascade Decomposition Method),当QP问题规模很大时,不能用现有的算法进行优化,因此提出了CDM方法,将大规模的QP问题分解为小规模的条件独立的QP问题,每一个小规模的QP问题都可以用现有的算法优化,且可以并行计算。
2. Related Work
sketch 一般有两种:profile(轮廓) 和 shading,后者效果更佳。
发展:
-
直接从training photos(没有分块)提取特征,线性合成sketch
缺点:photo 和 sketch 为两种类别的图,难以建立合适的线性关系。
-
考虑非线性的关系,进行分块。文献阅读003【精读】
缺点:由于每个sketch patch都是独立合成的(虽然有部分重叠),使其对于大规模的复杂的patches的合成效果明显降低。
-
考虑大规模的结构,MRF:对target photo 分块,对于每一个patch,从training sketch patches选出最佳的sketch patch,使其后验概率最大化。
缺点:如Introduction所说,不是合成新的sketch patches,NP-hard问题。
-
基于上面的MRF,先对脸部组成部分引入特定的形状,然后用SIFT特征来表示photo和sketch的每个patch。
该方法对光线的改变和姿势的变换有很强的鲁棒性,但是3的缺点还没有解决。
-
本论文的方法:MWF,针对3的缺点。
Large scale QP problems在计算机视觉有着很重要的应用和研究地位,最常用的方法为:分解成小规模的子问题。本论文提出基于马尔可夫特点的CDM方法。
3. Markov Weight Fields
联合概率:
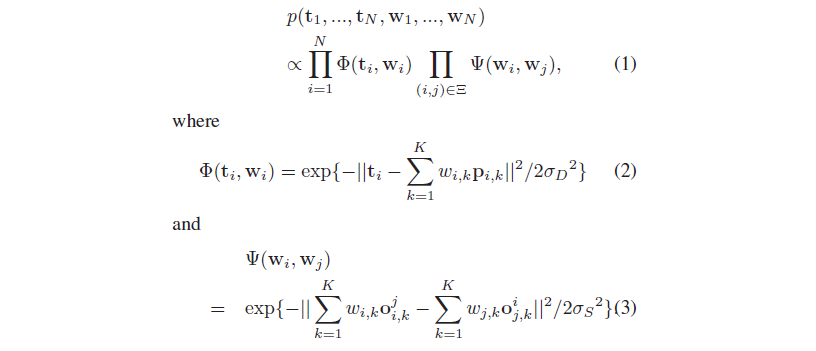
ti表示test photo patch的向量 L-vector(L=l²,l为 patch长和宽)
wi表示从training data提取出来的向量 K-vector
Pi表示从training photo patches提取出来的向量 K-vector,
Pi的元素,即Pi,k表示第k个候选的patch:L-vector
(i, j) ∈ Ξ 表示相邻结点
o_i,k^j 表示i,j之间的第k个候选patch的重叠面积
i=1,...,N
k=1,...,K
对于Φ,ti与Σwi,kPi,k越接近,说明拟合越好,此时Φ越接近1,符合逻辑。
对于Ψ,是基于马尔科夫性,仅考虑相邻两个结点(i,j)的相关性。
后验概率:
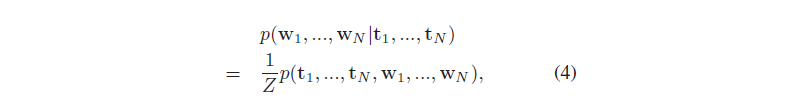
最大化后验概率,等价于最小化如下的损失函数:
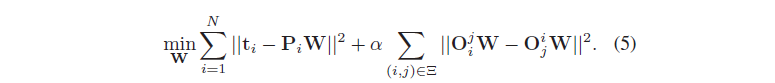
即,式(2),(3)的指数部分的相反数。
将其转化为QP问题(二次规划):
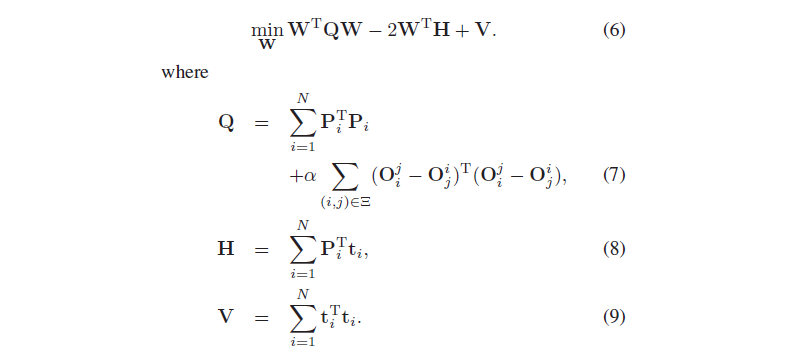
V其实是个常量,可以忽略。我们可以加上约束条件:Σ_k(wi,k)=1,wi,k>=0,即对wi归一化。
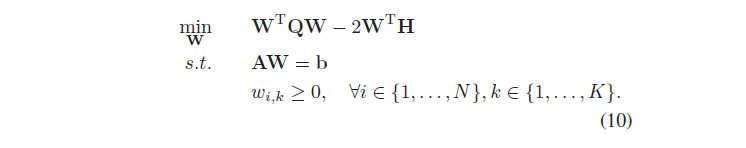
这里的A和b是对W归一化约束的矩阵和向量。
4. Cascade Decomposition Method
对于(10)的目标函数,由于W的维度太大(变量达到19000),没有合适的现成的优化算法。因此我们提出CDM,对W降维(使问题规模缩小为单个wi)。
我们对参数进行划分,
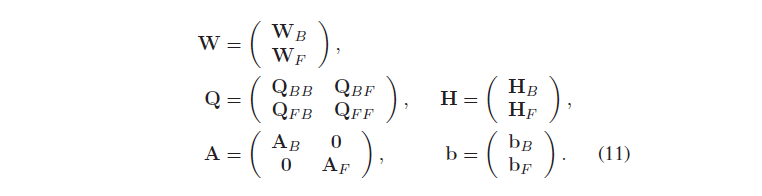
目标函数变成:
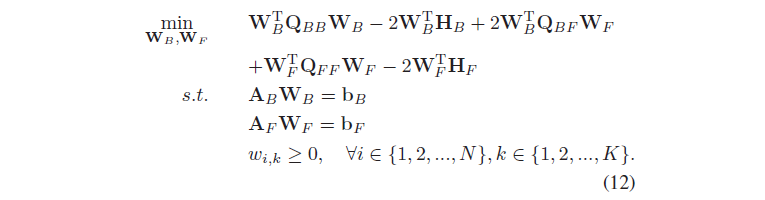
如何划分呢?
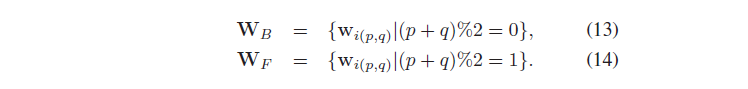
i(p,q)表示p行q列,这里就是要把相邻结点分开,这样,根据马尔科夫性,WB内的结点相互独立,就可以因子分解为wi(K-vector)。因此,目标函数可以分解为子问题:

wia是wi的相邻结点(4个),Qii,Qia,Hi,Ai是Q,H,A的分解因子。
算法:

Step1 , Step2可以并行执行,实验结果发现一般10次以内就会收敛。
5.Experiments
初步:
patch size = 20x20
overlapping area = 5x5
用 MWF 方法合成sketch 即按Algorithm1拟合出W。
优化:
patch size = 10x10
overlapping area = 5x5
K=10