2020牛客暑期多校训练营（第二场）B

题目链接：Boundary

题意：给你n个点，问最多有多少个点与原点(0,0)在同一个圆上

思路：由于三点确定一个圆，所以如果枚举剩余的两个点，然后再枚举其他点是否在圆上，那么复杂度为$O(n^3)$，会TLE

但我们可以利用$“$同弧所对的圆周角相等$”$这一性质，所以可以先枚举一个点P，然后枚举其他的点A，计算$angle OAP$，找到这些角里面角的众数即可，但是角相等只能说明弧相等，并不能保证这两段弧为同一段弧，例如下图，$angle OA_{1}P=angle OA_{2}P$，但这两段弧并不是同一段弧

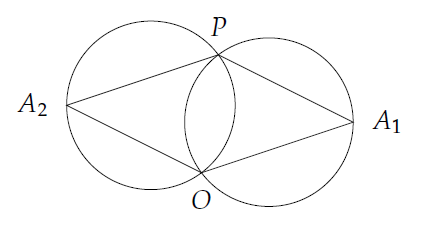
我们只需要计算一边，所以用叉积来判断即可，既满足$vec{OP} imes vec{OA}<0$或者$vec{OP} imes vec{OA}>0$

另一种方法：枚举两个点A，B，找到OA和AB中垂线的交点，这个交点就是圆心，计算圆心的众数即可，复杂度$O(n^2)$

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

const int N = 2010;
const double eps = 1e-10;

struct Vector {
    double x, y;
    Vector() { }
    Vector(double tx, double ty) : x(tx), y(ty) { }
};

int n;
pair<double, double> p[N];
double a[N], t;

inline double dot(Vector a, Vector b)
{
    return a.x * b.x + a.y * b.y;
}

inline double cross(Vector a, Vector b)
{
    return a.x * b.y - a.y * b.x;
}

inline double calc(Vector a, Vector b)
{
    double la = sqrt(a.x * a.x + a.y * a.y);
    double lb = sqrt(b.x * b.x + b.y * b.y);
    return acos(dot(a, b) / (la * lb));
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].first, &p[i].second);
    int res = 0, cnt = 0;
    for (int i = 1; i <= n; i++) {
        cnt = 0;
        for (int k = 1; k <= n; k++) {
            Vector op = Vector(p[i].first, p[i].second);
            Vector oa = Vector(p[k].first, p[k].second);
            Vector ap = Vector(p[k].first - p[i].first, p[k].second - p[i].second);
            Vector ao = Vector(p[k].first, p[k].second);
            if (cross(op, oa) < 0) a[++cnt] = calc(ap, ao);
        }
        sort(a + 1, a + cnt + 1);
        int imax = 0, c = 0;
        for (int i = 1; i <= cnt; i++) {
            if (fabs(a[i] - t) < eps) c++;
            else {
                c = 1;
                t = a[i];
            }
            imax = max(imax, c);
        }
        res = max(imax, res);
    }
    printf("%d
", res + 1);
    return 0;
}