Luogu-P1450 [HAOI2008]硬币购物-完全背包+容斥定理
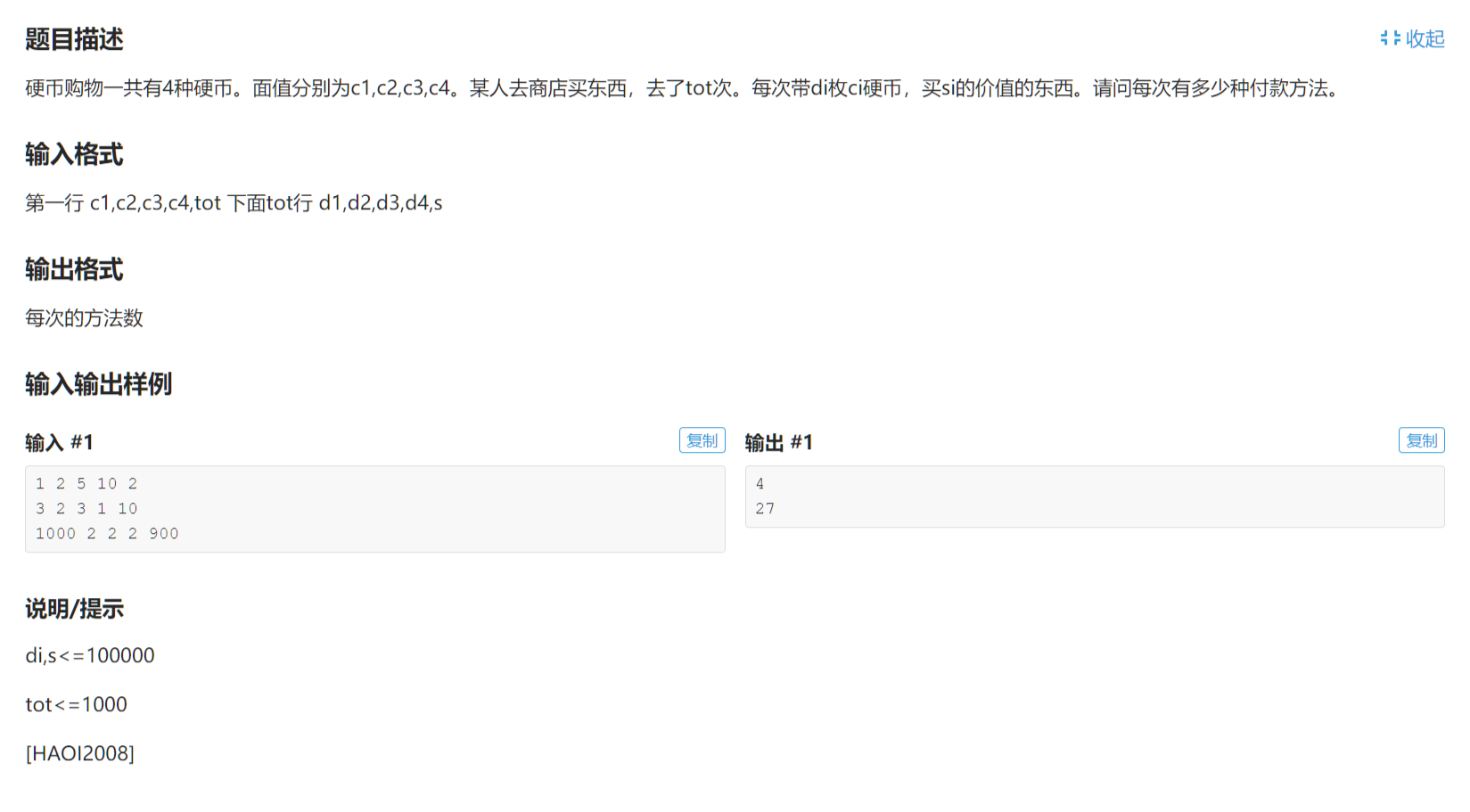
【Problem Description】
略
【Solution】
上述题目等价于:有(4)种物品,每种物品有(d_i)个,且每种物品的体积为(c_i),问有多少种方法装满容量为(s)的背包?可以很容易想到跑多重背包即可,但是发现复杂度为(O(4Vcdot n))。不可行。
题目要求的东西也等价于求以下等式有多少组满足条件的解:
如果学过容斥定理的,就可以看出来这是容斥定理的一个模型。
即先不考虑(x_1,x_2,x_3,x_4)的上界限制条件,即每种物品有无限多个,那么就可以跑完全背包求得所有的方案数,令(overline A_1,overline A_2,overline A_3,overline A_4)分别代表(0le x1le d_1, 0le x_2le d_2, 0le x_3le d_3, 0le x_4le d_4)的条件,那么我们要求的就是满足(overline A_1cap overline A_2cap overline A_3cap overline A_4)的方案数。有容斥原理公式得:
对于(|A_1|),我们知道(A_1Leftrightarrow x_1ge d_1+1)。所以(|A_1|)就表示(x_1ge d_1+1, x_2,x_3,x_4ge 0)时以下等式的解的个数:
令(z_1=x_1-(d_1+1),z_2=x_2,z_3=x_3,z_4=x_4),则原式变为在(z_1,z_2,z_3,z_4ge 0)的条件下,求以下等式解的个数:
预处理(10^5)以内容量为(i)方案数(dp[i])。则(|A_1|=dp[s-(d_1+1)])。同理(|A_i|=dp[s-(d_i+1)])。
对于(|A_1cap A_2|)等其他子集,也用类似方法转换为完全背包的做法。因为物品数只有(4)个,所以用位运算枚举子集,偶加奇数减即可。详细请看代码。复杂度为(O(4V+2^4cdot n))。
【Code】
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f
#define maxn 100005
int dp[maxn];
int c[5],d[5];
void CompleteBack(int V,int vol){ //完全背包
for(int j=vol;j<=V;j++){
dp[j]=dp[j]+dp[j-vol];
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>c[0]>>c[1]>>c[2]>>c[3];
dp[0]=1;
for(int i=0;i<4;i++){
CompleteBack(maxn-5,c[i]);
}
int n;cin>>n;
while(n--){
cin>>d[0]>>d[1]>>d[2]>>d[3];int s;cin>>s;
int ans=0;
for(int i=0;i<(1<<4);i++){ //枚举子集
int sum=s,num=0;
for(int j=0;j<4;j++){
if(i>>j&1){
sum-=c[j]*(d[j]+1); num++;
}
}
if(sum<0) continue;
if(num&1) ans-=dp[sum]; //偶加奇减
else ans+=dp[sum];
}
cout<<ans<<endl;
}
return 0;
}