最近公共祖先(LCA):
就是两个点在这棵树上距离最近的公共节点。
适用条件:
LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。一般节点数比较多,用最短路径的方法去解题一般会暴内存或暴空间
应用场景:
有一个性质,假设节点B和C的最近公共祖先是A,那么对于整个树的根节点D,
都有:|BD|+|CD|-|AD|*2=|BC|
用上述性质可以用来求BC两点之间的最短路径,前提是满足上面的使用条件(两点之家仅有唯一一条确定的路径)

如何求最近公共祖先
常用求LCA的算法有两种,即离线和在线两种算法,时间复杂度分别为O(n+q)、O(nlogn)。离线算法更好理解,代码量较少,用的比较多
在线算法有两种,RMQ和倍增。在线算法是输入一次询问处理一次,比离线算法更灵活,但是费时间。离线算法是一次性输入询问,将询问保存起来一次性处理,最后在一次性输出,时间复杂度更底。
一、离线算法
基本思路:
1.任选一个点为根节点,记为u,从根节点开始。
2.遍历该点u所有子节点v,并标记这些子节点v已被访问过。(正向遍历到底)
3.若是v还有子节点,返回2,否则下一步。
4.合并v到u上。
5.寻找与当前点u有询问关系的点v。(反向遍历到询问结束)。
如果节点v已经被访问过(vis标记过),那么u,v的最近共公共祖先就是点v的根节点,即 LCA(u,v)=fa(v)。
如果节点v未曾被访问过,跳过搜下一个点,当搜到点v时,在处理和点v有询问关系的点u,此时u,v的最近公共祖先就是点u的根节点,即LCA(u,v)=fa(u)。
eg:
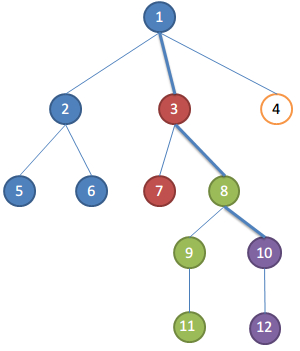
假设遍历完10的孩子,要处理关于10的请求了
取根节点到当前正在遍历的节点的路径为关键路径,即1-3-8-10
集合的祖先便是关键路径上距离集合最近的点
比如此时:
【1,2,5,6】为一个集合,祖先为1,集合中点和10的LCA为1
【3,7】为一个集合,祖先为3,集合中点和10的LCA为3
【8,9,11】为一个集合,祖先为8,集合中点和10的LCA为8
【10,12】为一个集合,祖先为10,集合中点和10的LCA为10
可以发现集合的祖先便是LCA !
伪代码:
Tarjan(u)//join和find为并查集合并函数和查找函数 { for u节点的所有子节点 //访问所有u子节点v { Tarjan(v); //继续往下遍历 join(u,v); //合并v到u上 标记v被访问过; } for 查询节点的所有子节点 //访问所有和u有询问关系的e { 如果e被访问过; u,e的最近公共祖先为find(e); } }
没看懂?模拟过程:https://www.cnblogs.com/JVxie/p/4854719.html
模板题:求最近祖先节点 https://www.cnblogs.com/-citywall123/p/11012695.html
模板题应用:求两点之间最短距离 https://www.cnblogs.com/-citywall123/p/11065033.html
二、在线算法: