Description
为了让奶牛们娱乐和锻炼,农夫约翰建造了一个美丽的池塘。这个长方形的池子被分成了M行N列个方格(1≤M,N≤30)。一些格子是坚固得令人惊讶的莲花,还有一些格子是岩石,其余的只是美丽、纯净、湛蓝的水。
贝西正在练习芭蕾舞,她站在一朵莲花上,想跳到另一朵莲花上去,她只能从一朵莲花跳到另一朵莲花上,既不能跳到水里,也不能跳到岩石上。
贝西的舞步很像象棋中的马步:每次总是先横向移动一格,再纵向移动两格,或先纵向移动两格,再横向移动一格。最多时,贝西会有八个移动方向可供选择。
约翰一直在观看贝西的芭蕾练习,发现她有时候不能跳到终点,因为中间缺了一些荷叶。于是他想要添加几朵莲花来帮助贝西完成任务。一贯节俭的约翰只想添加最少数量的莲花。当然,莲花不能放在石头上。
请帮助约翰确定必须要添加的莲花的最少数量,以及有多少种放置这些莲花的方法。
Input
第一行:两个用空格分开的整数:M和N
第二行到M+1行:第i+1行有N个用空格分开的整数,描述了池塘第i行的状态:
0为水,1为莲花,2为岩石,3为贝西所在的起点,4为贝西想去的终点。
Output
第一行:一个整数,需要增加的最少莲花数;如果无解,输出-1。
第二行:放置这些莲花的方案数量,保证这个数字不会超过一个64位的有符号整数,
如果第一行是-1,不要输出第二行。
这道题不错啊,表示很考思维.
首先,我们需要知道放多少莲花,如何放.
因此考虑最短路,方案数,我们就考虑最短路计数.(想信大家都会的)
这题的难点在于如何建边.
因为贝西可以跳任何一个位置,(任何一个有水的位置都可以放莲花)
所以我们不能单纯地从起点开始向其他点连边,所以我们要从每一个有水的地方开始.
由于岩石对答案没有贡献,所以不考虑连边.
多次(dfs)对整个图连边.
既然想到这了,你可能会发现,这是一个二维的最短路,记录状态不太好记录.
因此我们给每一个格子编号,像这样.
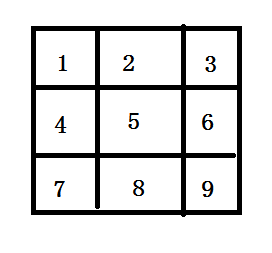
当然,还有其他编号方法,这样比较简单罢了.
算某一位置((x,y))的编号的话,式子为(idx[x][y]=(x-1) imes m+y)
这样建边操作就简单多了.
然后后面只需要敲一个裸的最短路和最短路计数问题就好了.
输出添加的荷花的最小的数量的时候要(-1)
这是因为,这个数量实际上是点权,而我们跑最短路用的是边权.
一个点与两条边相连,所以要(-1)。
代码
#include<cstdio>
#include<cctype>
#include<queue>
#include<cstring>
#define int long long
#define clear(a,b) memset(a,b,sizeof a)
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,m,res[35][35],tot,idx[35][35],dis[1008611];
int sx,sy,fx,fy,s,t,head[1008611],to[1008611];
const int ax[]={2,1,-1,-2,2,1,-1,-2};
const int ay[]={1,2,2,1,-1,-2,-2,-1};
bool vis[35][35],inq[1008611];
struct coc{int u,v;}edge[1008611];
inline void add(int x,int y)
{
edge[++tot].u=head[x];
edge[tot].v=y;
head[x]=tot;
}
void dfs(int id,int x,int y)
{
if(vis[x][y])return;
vis[x][y]=true;
for(R int i=0;i<8;i++)
{
R int nx=x+ax[i],ny=y+ay[i];
if(nx<1 || nx>n || ny>m || ny<1 || vis[nx][ny])continue;
//刚开始写成return,尴尬死了 emm
if(res[nx][ny]==1)dfs(id,nx,ny);
else if(res[nx][ny]!=2)
{
vis[nx][ny]=true;
add(id,idx[nx][ny]);
}
}
}
inline void spfa()
{
queue<int>q;
for(R int i=1;i<=n*m;i++)dis[i]=2147483647;dis[s]=0;
inq[s]=true;q.push(s);to[s]=1;
while(!q.empty())
{
int u=q.front();q.pop();inq[u]=false;
for(R int i=head[u];i;i=edge[i].u)
{
if(dis[edge[i].v]>dis[u]+1)
{
dis[edge[i].v]=dis[u]+1;
to[edge[i].v]=to[u];
if(!inq[edge[i].v])
{
q.push(edge[i].v);
inq[edge[i].v]=true;
}
}
else if(dis[edge[i].v]==dis[u]+1)
to[edge[i].v]+=to[u];
}
}
if(dis[t]<2147483647)printf("%lld
%lld",dis[t]-1,to[t]);
else printf("-1");
}
signed main()
{
in(n),in(m);
for(R int i=1;i<=n;i++)
for(R int j=1;j<=m;j++)
{
in(res[i][j]);
idx[i][j]=(i-1)*m+j;
if(res[i][j]==3)sx=i,sy=j;
if(res[i][j]==4)fx=i,fy=j;
}
for(R int i=1;i<=n;i++)
for(R int j=1;j<=m;j++)
if(!res[i][j] or res[i][j]==3)
clear(vis,0),dfs(idx[i][j],i,j);
s=idx[sx][sy];t=idx[fx][fy];
spfa();
}