贝叶斯决策和MAP分类器
后验概率 p(Ci|x) 表达给定模式 x 属于类 Ci 的概率。
模式 x 属于类 Ci 的后验概率计算公式为:
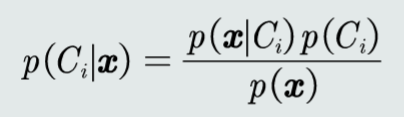
MAP分类器:将测试样本决策分类给后验概率最大的那个类。
判别公式:
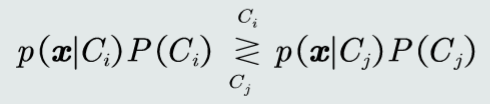
对于二分类问题,MAP分类器的决策边界:
单维空间:通常有两条决策边界。
高维空间:复杂的非线性边界。
决策误差:
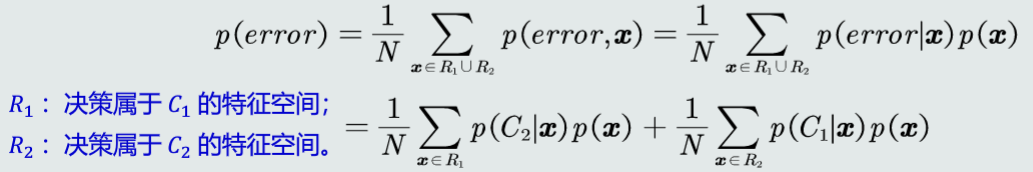
决策风险和贝叶斯分类器
决策风险的概念:不同的决策错误会产生程度不同的风险。
损失:

决策风险的评估:

贝叶斯分类器:
选择决策风险最小的类。
判别公式:

决策损失:
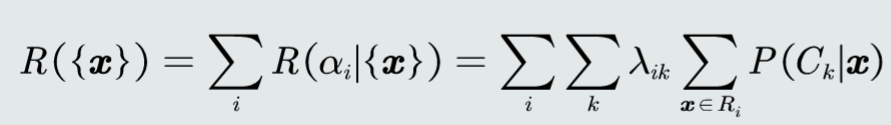
简化特征维度:

最大似然估计
定义:
- 待学习的概率密度函数记为 p(x | θ),θ 是待学习的参数。
- 给定的 N 个训练样本都是从 p(x | θ) 采样得到的,且满足iid条件,则所有样本的联合概率密度(似然函数)为:
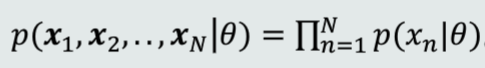
- 因此,学习参数 θ 的目标函数可以设计为:使该似然函数最大。
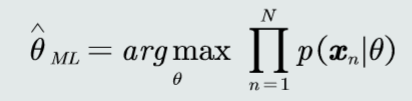
贝叶斯估计
贝叶斯估计:给定参数 θ 分布的先验概率以及训练样本,估计参数 θ 分布的后验概率。
θ 的后验概率:

KNN估计
给定 N 个训练样本,在特征空间内估计每个任意取值 x 的概率密度,即估计以 x 为中心,在极小的区域 R = (x, x+δx) 内的概率密度 p(x)
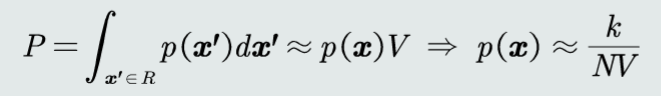
其中 k 为落入区域 R 的样本个数,V 为区域 R 的体积。
直方图
直方图也是基于无参数概率估计的基本原理:p ≈ k/(NV)
将特征空间划分为 m 个区域R。
给定任意模式,先判断它属于哪个区域,p(x) = ki/(NV), if x ∈ Ri
优点:
- 固定区域 R:减少由于噪声污染造成的估计偏差。
- 不需要存储训练样本。
缺点:
- 固定区域 R 的位置:如果模式 x 落在相邻格子的交界区域,意味着当前格子不是以模式 x 为中心,导致统计和概率估计不准确。
- 固定区域 R 的大小:缺乏概率估计的自适应能力,导致过于尖锐或平滑。