消木块(模型(设计消除后效性))⭐

题面

你们中的一些人可能玩过一个叫做消木块的游戏。

n个木块排成一列，每个木块都有一个颜色。

例如下图中木块的颜色分别为：金，银，银，银，银，铜，铜，铜，金。

每次，你都可以点击一个木块，这样被点击的木块以及和它相邻并且同色的木块就会消除。

如果一次性消除了k个木块，那么就会得到k*k分。

例如下图所示，点击银色木块，四个木块被消去，得到16分。

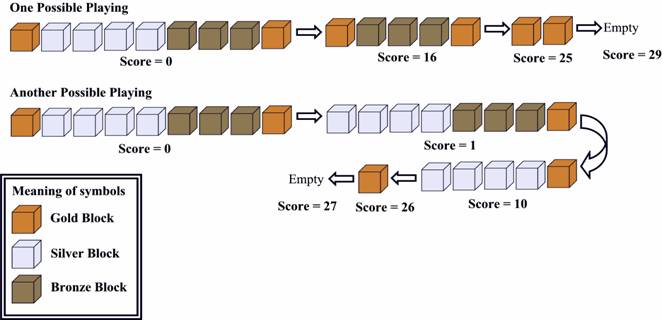
给定你一个游戏初始状态，请你求出最高得分是多少。

输入格式

第一行包含整数t，表示共有t组测试数据。

每组数据第一行包含整数n，表示共有n个木块。

第二行包含n个整数，表示n个木块的颜色。

代表木块颜色的整数范围是1~n。

输出格式

每组数据输出一个结果，每个结果占一行。

输出格式为“Case x: y”，其中x为数据组别编号，从1开始，y为结果。

数据范围

1≤n≤200

输入样例：

2
9
1 2 2 2 2 3 3 3 1
1
1

输出样例：

Case 1: 29
Case 2: 1

题解

如果是普通的区间dp,那么f[left][right]就完事了

可惜这道题不是,如果用普通的一维区间dp,是状态转移有问题的

因为你拼接的时候,可以有多种方式

所以因改为 f[left][right][t] 表示 right ~ right + t, a[i] == a[right] (颜色相等)

则转移分三种

`.left ~ right 颜色都一样 则 f[l][r] = sqr(r - l ~ 1)

2.否则枚举 left ~ k (k < right - 1), 且 a[p] = a[k + 1] && a[p + 1] != a[k + 1]

就是先枚举出 拼接点 k 和 k + 1, 然后从 k 向 left 消方块直到存在一个方块可以和(k+1)削去, 即枚举每个和(k+1)颜色相同区间的右端点,去转移

3.不枚举p了,直接消除 (k+1)所在区间(颜色相同)转移

代码如下

#include <bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define per(i,a,b) for(int i=a;i>=b;--i)
#define sqr(n) (n)*(n)
using namespace std;

const int maxn = 205;

int _, n, m;
int a[maxn], f[maxn][maxn][maxn];

int dp(int i, int j, int k) 
{
    int& cur = f[i][j][k];
    if(cur >= 0) return cur;
    cur = 0;
    
    int p = j;
    for(; p - 1 >= i && a[p - 1] == a[j]; --p);
    if(p == i) return cur = sqr(j - p + 1 + k);
    
    rep (q, i, p - 1)
        if(a[q] == a[j] && a[q+1] != a[j])
            cur = max(cur, dp(q + 1, p - 1, 0) + dp(i, q, j - p + 1 + k));
            
    return cur = max(cur, dp(i, p - 1, 0) + sqr(j - p + 1 + k));
}

int main()
{
    ios::sync_with_stdio(0); cin.tie(0);
    for (cin >> _; _; --_)
    {
        cin >> n; memset(f, -1, sizeof f);
        rep (i, 1, n) cin >> a[i];
        cout << "Case " << ++m << ": " << dp(1, n, 0) << '
';
    }
    return 0;
}