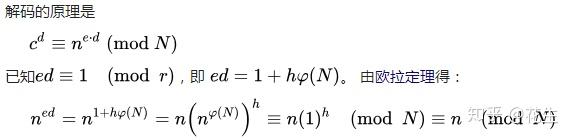私钥算法
私钥加密算法(对称加密算法),因为解密密钥和加密密钥是相同的,所以这个密钥是不能公开的,不然的话就相当于是明文了。常见的对称加密算法有:DES、3DES、AES、DESX、Blowfish、RC4、RC5、RC6
公钥算法
公钥加密算法(非对称加密算法),这种算法加密和解密的密码不一样,拥有公钥和私钥:
- 公钥和私钥成对出现
- 公钥和私钥是相对的,并没有限制谁只能是公钥,只是我们将公开的密钥叫公钥,私有的叫私钥
- 用公钥(私钥)加密的数据只有对应的私钥(公钥)可以解密
- 公钥(私钥)只能解对应私钥(公钥)加密的数据
常见的非对称加密算法有:RSA、DSA(数字签名用)、ECC(移动设备用)、Diffie-Hellman、El Gamal
数据安全
不管是对称加密还是非对称加密算法,它的作用其实都是为了保证数据的安全。但是这两种算法加密之后的数据是不是就是完全安全的呢?
优劣对比
对称加密:
- 算法公开,安全性较低
- 计算量小,加密解密效率高
- 密钥管理分发困难,不够安全
非对称加密:
- 加密解密使用不同密钥,安全性较高
- 加密解密效率较低,花费时间较长
我们常见的数字证书和加密狗多采用非对称的加密算法。但是在实际业务中,尤其是数据量较多的情况下,非对称加密的效率较低,所以常见的是使用对称加密+非对称加密的方法。
非对策的算法分析
对称加密的理解比较简单,不做什么记录,简单的说就是怎么来的怎么回去。这里记录一下RSA加密算法:
数学基础
在学习RSA加密算法之间,我们需要理解以下的数学基础:
- 质数:在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
- 合数:大于1的自然数,不是质数。
- 分解质因数:每一个合数都可以以唯一形式被写成质数的乘积。
- 互质:公约数只有1的两个整数,叫做互质整数。公约数只有1的两个自然数,叫做互质自然数。
- 欧拉函数:O(n),小于或等于n的正整数中与n互质的数的数目。
- 模反元素:如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。这时,b就叫做a的“模反元素”。比如a=3,n=11;则b=4。实际上4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…},即b+kn都是a的模反元素。
- 同余:两个整数a,b,若它们除以正整数m所得的余数相等,则称a, b对于模m同余,如26等于14(mod12)。
- 欧拉定理:即a的O(n)次方与1在模n下同余;O(n)为欧拉函数。如上n=11,O(n)=10,a的O(n)次方为3的10次方等于=59049=(5368*11 + 1)。
RSA原理
RSA加密算法是一种非对称加密技术,基本原理是将两个很大的质数相乘很容易得到乘积,但是该乘积分解质因数却很困难。
公钥私钥的生成
1.选择两个大质数p和q,p不等于q,计算出N=p*q
2.根据欧拉函数,任何质数p的互质数目为p-1,另r=O(N)=O(p)O(q)=(p-1)(q-1)
3.选择一个小于r的整数e,另r和e互质,求e关于r的模反元素为d。
4.(N, e)为公钥;(N,d)为私钥。
比如p=11, q=2; 则N=22, r=10。 选择e=3, d可以为7,17,27(7+10k)
公钥为(22, 3), 私钥为(22, 7)。
注意:公钥私钥没有明确指定,可以公钥为(22, 7), 私钥为(22, 3)。
数据加密
原始信息为n,加密动作为:
c = n的e次方 (mod N)
如上例,原始数据6,6的3次方为216, (mod 22) 后为18
注:原始数据n必须小于N,当p和q足够大的时候是没问题的
数据解密
现在要通过c和私钥(N,d)将c解密出n。
c的d次方 = n (mod N)
如上例 18的7次方=612220032,(mod 22)后为6; 18的17次方2185911559738696531968,(mod 22)后22也为6