昨天参加今日头条和58转转的笔试,因为时间上有冲突,所以主要选择参加头条的笔试。
先说头条:
头条的题型:
一道改错题
三道编程题
一道设计题
感受:
做题目的的时候还是有点紧张的,因为突然遇到题目需要思考很长时间,而且不确定是否正确时,真的是着急。
做完头条笔试感觉真是好大差距,有大神三道编程全部AC,而我三道编程只能50%,0,0;
改错题一上来有点懵,半个多小时,最后还不知道改的对不对。
设计题基本是用一个套路来回答的,也不确定,但肯定不完善。
被虐的体无完肤。
下面主要记一下编程题:
第一题有思路,但是不知道哪里出的问题,最后只有50%通过。后来了解到,可能是输入输出使用cin/cout所致,在数据量比较大的时候使用scanf和printf效率会比较高。
但是第一题花费了过长的时间,大概接近50分钟。真的需要多写代码,熟练基本容器的使用。不然在写的时候,就会发现自己的代码上真的还是存在很大问题的。容器,迭代器。
第二题,因为只剩下十几分钟,刚开始题目都没有理解透。最后才读明白,可以用线段树。
第三题,直接没有时间去看。
下面贴一下大神的思路:
作者:Ck0123 链接:https://www.nowcoder.com/discuss/33986 来源:牛客网
总结:对于容器的使用要很重视,经常遇到同一类型需要用到pair容器的题目;
要提高编码的速度和质量,对于第一个题目,因为粗心可能浪费了有二十分钟调试。思路没有问题,都花在改代码上。。。
面对这样的编程笔试题目,一般,我觉得一道题目花费时间不应该超过25分钟。所以,当你在一道有思路的题目上花费超过半小时,那就说明你编码功底不够。
另外,面对题目吐过没有思路,说明对与常见算法与题目熟练度不够,需要多加练习。
实现代码,陆续补上!
1. 先上第一道改错题,感受一下:
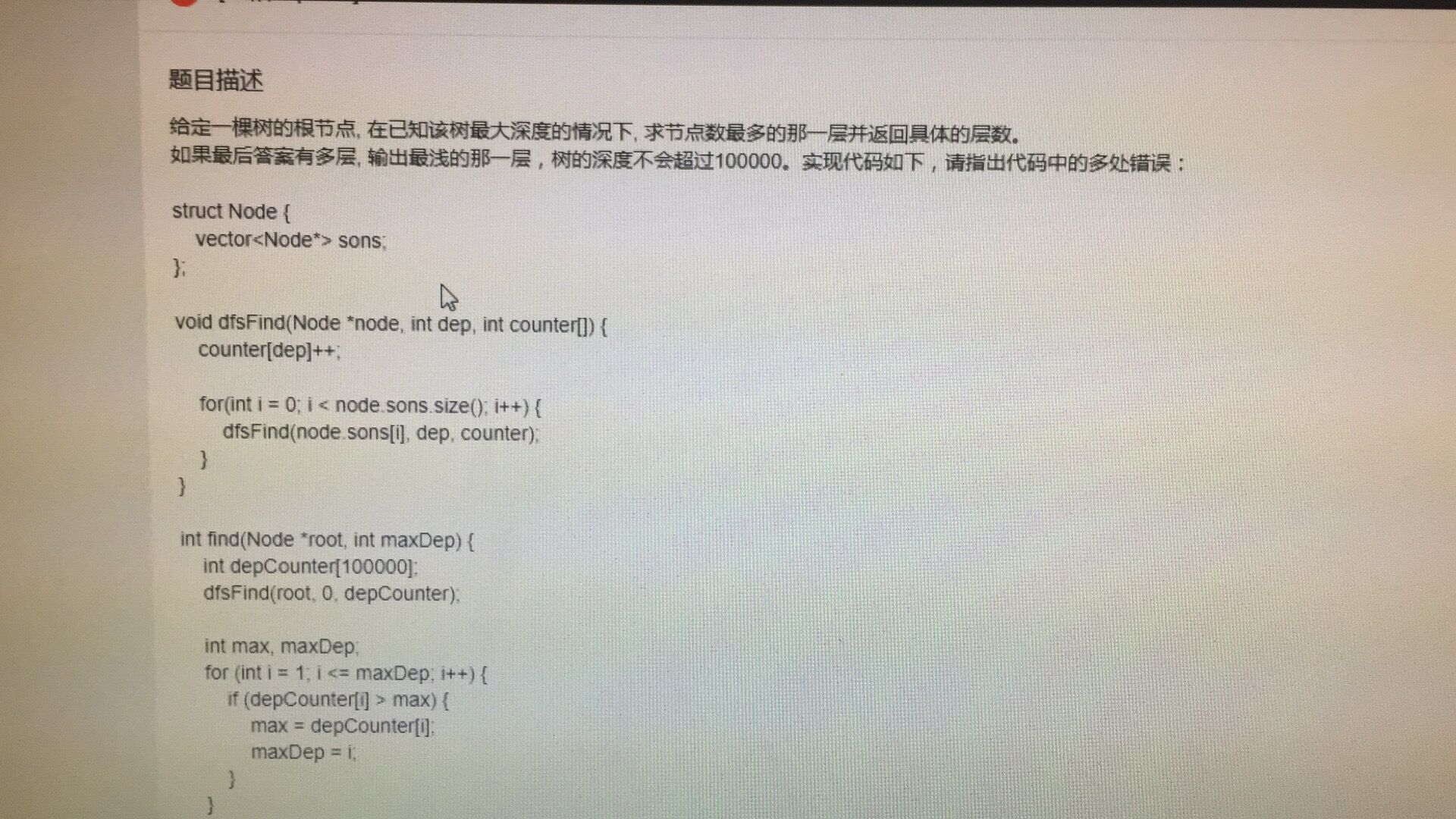
改错如下:
作者:苏uu
链接:https://www.nowcoder.com/discuss/34136
来源:牛客网
dfsFind()函数
1. 没有处理node为空的边界条件;(我没考虑到)
2. 函数内的循环中node类型为Node*调用sons应为node->sons.size()和node->sons[i]; (考虑到了)
3. 函数递归调用是dep+1(考虑到了)
修改如下:
void dfsFind(Node* node, int dep, int counter[]) {
if(node == nullptr) return;
counter[dep]++;
for(int i = 0; i < node->sons.size(); i++){
dfsFind(node->sons[i], dep + 1, counter);
}
}
find函数中:
1. 树的深度最大为100000,则保存树各个深度的数组大小应为100001,且数组没有初始化,改为depCounter[100001] = {0}; (考虑到了)
2. 函数内用来记录最大节点的数目和的变量没有初始化,且记录最多节点所在的层数的变量明与maxDep同名,修改变量名为maxNodeLevel; (同名也考虑了,但是没有修改)
修改如下:
int find(Node* root, int maxDep)
{
int depCounter[100001] = {0};
dfsFind(root, 0, depCounter);
int max = 0;
int maxNodeLevel = 1;
for(int i = 1; i < maxDep; i++) {
if(depCounter[i] > max){
max = depCounter[i];
maxNodeLevel = i;
}
}
return maxNodeLevel;
}
2. 编程第一题:

我的实现代码(AC 50%)如下:
#include <iostream> #include <vector> #include <algorithm> #include <math.h> #include <string> using namespace std; int find(vector<int> vec, int m){ int res; for (int i = 0; i < vec.size(); i++){ if (m == vec[i]){ return i; } } } int main(){ int N; cin >> N; int x, y; //vector<pair<int, int>> vec; vector<int> X; vector<int> Y; for (int i = 0; i < N; i++){ cin >> x >> y; X.push_back(x); Y.push_back(y); } vector<int> X2(X); vector<int> Y2(Y); vector<int> res_x; vector<int> res_y; sort(Y2.begin(), Y2.end()); for (int j = 0; j < Y.size(); j++){ if (Y2[Y.size()-1] == Y[j]){ res_x.push_back(X[j]); res_y.push_back(Y[j]); break; } } int temp = 0; for (int i = Y2.size()-2; i>=0; i--){ int res=find(Y, Y2[i]); if (X[res]>res_x[temp]){ res_x.push_back(X[res]); res_y.push_back(Y[res]); temp++; } } int len = res_x.size(); //cout << len << endl; for (int i = 0; i < len; i++){ cout << res_x[i] << " " << res_y[i] << endl; } system("pause"); return 0; }
思路好像正确,话说是因为cin/cout速度慢应该替换成scanf/printf.
等一个100%的代码;
我的改进版本:
#include<iostream> #include<stdio.h> #include<vector> #include<algorithm> using namespace std; bool cmp(const pair<int, int> p1, const pair<int, int> p2){ return p1.second > p2.second; //这样是从大到小排序了; } int main(){ int n; //cin >> n; scanf("%d", &n); vector<pair<int, int>> vec; int x, y; for (int i = 0; i < n; i++){ //cin >> x >> y; scanf("%d %d", &x, &y); vec.push_back(make_pair(x, y)); } sort(vec.begin(), vec.end(), cmp); vector<pair<int, int>> res; res.push_back(make_pair(vec[0].first, vec[0].second)); //cout << res[0].first << " " << res[0].second << endl; int temp = 0; for (int i = 1; i<n; i++){ if (vec[i].first > res[temp].first){ res.push_back(make_pair(vec[i].first, vec[i].second)); temp++; } } int len = res.size(); for (int i = 0; i < len; i++){ //cout << res[i].first << " " << res[i].second << endl; printf("%d %d ", res[i].first, res[i].second); } system("pause"); return 0; }
2. 编程第二题:

题目是求解区间最大值,第一个应该想到的高效方法就应该是线段树。
后来知道 这是个原题,POJ2796 使用单调栈,O(N)时间即能解决。
1)单调栈的思路:
Solution : 枚举+单调栈。看别人的解题报告学习了。单调栈这么厉害。对于这种题目,我们不能枚举区间(肯定超时),所以只能枚举最小值这个点,看看以这个点为最小值的区间向左和向右能伸展多远。这才是正确的思路。那么有了这个思路,如何实现呢。我们考虑单调栈!从第一个元素到最后一个元素一个一个入栈,我们发现,如果当前元素大于栈顶元素,那么这个元素是不能向前伸展的;同时如果当前元素小于栈顶元素,这个时候就要把栈中的元素一个一个弹出来,对于弹出来的元素,它扩展到当前元素就不能向后伸展下去了,因此对于弹出来的元素这个时候就可以计算左右端点形成区间与最小值的乘积了,维护一个最大值就好了,而对于当前元素的向前伸展端点就是新维护的栈顶元素的后一个元素了。这个题目有两个要注意的地方,第一,要手动在序列的最后加上一个-1。这样是为了能使得所有的元素都能入栈出栈。第二,对于序列中相等的元素,直接忽略就好了,其实这也是把相等的元素看成一个元素,最后计算的时候用的前缀和减前缀和,因此是可以计算到这些相等的元素的(并没有真正忽略!)。
#include <stdio.h>
#include <string.h>
const int MAXN=100000+5;
typedef long long LL;
int n;
LL a[MAXN];
LL stack[MAXN],top;
LL left[MAXN],sum[MAXN];
int main()
{
//freopen("in","r",stdin);
while(~scanf("%d",&n)){
top=sum[0]=0;
LL ans=-1,ansL=0,ansR=0;
for(LL i=1;i<=n;i++)
scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i];
a[++n]=-1;
for(LL i=1;i<=n;i++){
if(!top||a[i]>a[stack[top-1]]){
stack[top++]=i;
left[i]=i;
continue;
}
if(a[i]==a[stack[top-1]])
continue;
while(top>0&&a[i]<a[stack[top-1]]){
top--;
LL tmp=a[stack[top]]*(sum[i-1]-sum[left[stack[top]]-1]);
if(tmp>ans)
ans=tmp,ansL=left[stack[top]],ansR=i-1;
}
LL tmpL=stack[top];
stack[top++]=i;
left[i]=left[tmpL];
}
printf("%lld
%lld %lld
",ans,ansL,ansR);
}
return 0;
}
2)另一种,基于线段树的思路:
题解:思路来源于【http://acm.hdu.edu.cn/showproblem.php?pid=1506】这个题。
思想是:一a[i]为某个区间的最小值,初始区间为[i,i],左端向左延伸,右端向右延伸。最后维护最大值。
但是向前向后延伸的时候不能暴力,时间不允许,这里要用到DP的思想:
定义L[MAXN]=R[MAXN]=i;对于a[i]的L[i],刚开始的L[i]=i;如果a[i]>a[L[i]-1] -> L[i]=L[L[i]-1];2、R同理。
#define _CRT_SECURE_NO_WARNINGS
#include<cstdio>
#include<stdio.h>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 100050;
LL a[MAXN], sum[MAXN];
LL L[MAXN], R[MAXN];
int n;
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%lld", &a[i]);
sum[i] = sum[i - 1] + a[i];
L[i] = R[i] = i;
}
a[0] = a[n + 1] = -1;//保证不会访问或者访问无效。
for (int i = 1; i <= n; i++)
{
while (a[i] <= a[L[i] - 1])
L[i] = L[L[i] - 1];
}
for (int i = n; i >= 1; i--)
{
while (a[i] <= a[R[i] + 1])
R[i] = R[R[i] + 1];
}
LL ans = -1, l, r;
for (int i = 1; i <= n; i++)
{
LL T = a[i] * (sum[R[i]] - sum[L[i] - 1]);
if (ans < T)
ans = T, l = L[i], r = R[i];
}
printf("%lld
%lld %lld
", ans, l, r);
system("pause");
return 0;
}
下面再说58转转。