第二次作业——个人项目实战
标签(空格分隔): 软工实践
github的传送门:work2、work2-附加题2
题目的传送门
上次作业的评分总结
一、解题思路
看到题目的一反应就是:在不考虑效率的前提下,这题搜索是一定可以做的。
但是有要求:
25分为正确性评分,正确性测试中输入范围限制在 1-1000,要求程序在 60 s 内给出结果,超时则认定运行结果无效。
10分为性能评分,性能测试中输入范围限制在 10000-1000000,没有时间的最小要求限制。
所以普通的搜索应该是不行的,但是思考一下,如果使用回朔法(暴力+剪枝)效果怎么样呢?因为回溯的时间复杂度比较玄学,我不敢下定论,
思考了一会后,我觉得,数独应该是一个比较成熟的项目,应该可以比较容易的找到与其生成方法的相关资料。
百度了之后,发现提到的数独生成算法,大部分都是用类似'换行换列'之类的思想:先预处理生成或者直接手动输入一个数独,然后进行交换,这样子就可以生成新的数独.
好像很有道理的样子,所以我决定,搜索和上面提到的这个算法都实现一下,比比效率和实现的难易程度(这个时候我把自己坑到了,我一直以为数独是同行同列不能重复数字,没有注意到同九宫格也不能重复数字,也没有仔细看题,所以一开始的思路也是错的,但是误打误撞还真分析了出了点东西)。
为了体现随机性,我使用随机排列函数random_shuffle来随机第一行的数字1~9的填放方法。
那么问题来了,这样子的随机对搜索来说,搜索的起点变了,但搜索的终点(如果需要全部搜索完毕的话)是不会变的,因此会造成搜索到的方法数变小,那么会不会出现比作业需求的方案数少的情况呢?
从数独-- 一个高效率生成数独的算法中我得知,数独方案数约有6.67×10的21次方种,因此,第一排的随机,即使最坏情况下:生成的第一排的排列为1~9的逆序:
9 8 7 6 5 4 3 2 1
但即使如此,方案数最坏情况下是:上述的数字除以9的阶乘,回溯能查询到的方案数依然远大于于题目的需求。
而'换行换列'的方法,更不会局限于此。
搜索的方法很简单:把9*9的方格用081来标号,暴力的从1081依次填入19,(08事先填好了),每填一个数字前先判断一下填入当前的数字是否满足填入规则:不能与已经填入的格子的数字产生冲突,如果可行,就选择下一个格子继续填,不行就放弃这个方案,很裸的暴力,思考量很小。
关于'换行换列':由于本人的不认真查阅资料和阅读,我只看见了这一句话没认真思考便动手碰起了键盘
于是我产生了一个看上去比较WS的算法,思路如下,我先写一个数独出来,用二维数组A表示,然后再生成一个乱序的1-9一维数组,用一维数组b表示。
--from 数独-- 一个高效率生成数独的算法
我是想先生成一个数独,再用用了全排列函数,想通过全排列函数来生成新的排列来达到生成新数独的目的。
(当然...后面发现我这样子想实际上是错的= =...)
二、设计实现
1、函数设计
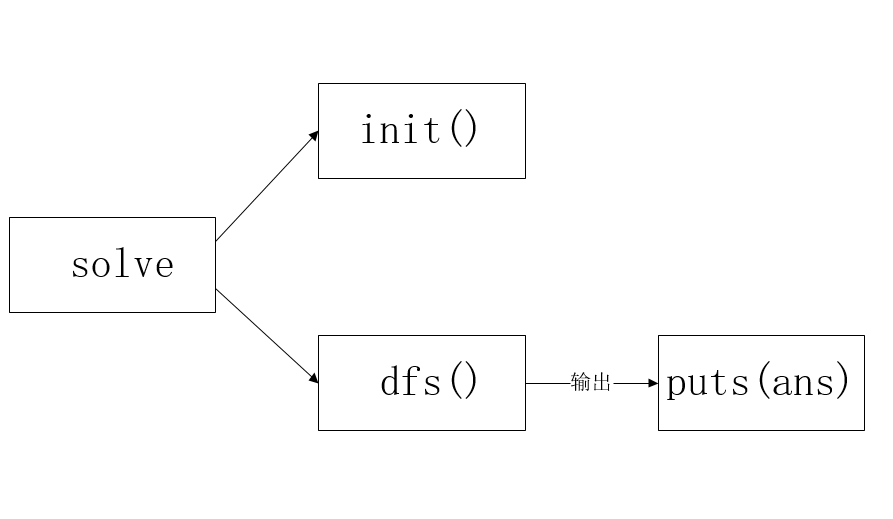
设想用一个函数solve()来全局的处理,期间调用一个init()函数来初始化所有需要用到的变量,然后通过dfs()函数来进行回溯和搜索操作,并且在dfs()函数中来输出方案。
形式如下:
void solve()
{
init();
.......
dfs(10); //回溯,暴搜+剪枝
}
dfs()函数需要完成三个功能:递归、剪枝、方案的输出。
其中剪枝又有两种:无效方案的去除以及搜索了足够多(满足输入需求)的方案后的剪枝。
形式如下:
void dfs(int t)
{
if (flag) return;
if (t>81)
{
....//输出方案
if 输出了n个方案 flag = true;
return;
}
rep(i, 1, 10) //当前选择可以放的数字
{
if 不满足条件 continue;
.....//递归
}
}
2、类设计
类的设计我一开始没有考虑到,因为我的函数关系相对比较简单,直接写即可。
后来加上了一个 generator类,把上述函数封装了起来,然后给solve()函数传递一个参数n,表示方案数,这样子就可以不受main的输入方式(XX.exe -c num or 直接运行exe输入)的干扰。
三、代码说明
1.随机排列的实现
题目的输出要求是:
随机生成N个不重复的已解答完毕的数独棋盘.
随机如何体现?(我觉得实际上肯定没有随机这个测试点),输入同一个N如何让输出的答案不完全相同呢?单纯的搜索是做不到的。做法就是用随机函数来实现。但是C++的STL有封装了类似的功能,就是用random_shuffle(begin(),end())来将其中的元素随机打乱顺序。
//初始化1~9
rep(i, 0, 10) ways[1][i] = i + '0';
//尾号48,48%9+1 = 4,第一个位置要是4
swap(ways[1][1], ways[1][4]);
//实现随机全排列,随机的关键
random_shuffle(ways[1] + 2, ways[1] + 10);
2.搜索过程
搜索的需要三组标记:行标记、列标记、九宫格标记,表示某行、列..哪些数字已经使用过了。
int x = (t - 1) / 9 + 1; //当前搜索到哪个格子
int y = (t - 1) % 9 + 1;
int p = belong[x][y]; //当前格子属于哪一个九宫格
rep(i, 1, 10) //当前选择可以放的数字
{
//当前行、列、九宫格中使用过
if (row[x][i] || col[y][i] || vis[p][i]) continue;
//标记
row[x][i] = col[y][i] = vis[p][i] = true;
ways[x][y] = i + '0';
//下一个格子
dfs(t + 1);
//去标记
row[x][i] = col[y][i] = vis[p][i] = false;
}
3.输出方式
经过优化后的输出方式,有一点巧妙,用puts()输出,用字符串表示方案,一个方案一次输出,可以快很多
预处理部分
//预处理出输出格式
cnt = 0;
rep(i, 1, 10)
{
//一个数字,一个空格
rep(i, 1, 9) put[cnt++] = 'X', put[cnt++] = ' ';
//行末无空格
put[cnt++] = 'X'; put[cnt++] = '
';
}
put[--cnt] = '�';//最后一行后无'
';
实际输出部分
if (ans++) puts(""); //两个方案之间有空格
cnt = 0; //初始化
rep(i, 1, 10) rep(j, 1, 10) //for循环遍历每个格子
{
//两个数字之间的空格还是换行已经预处理过了
put[cnt++] = ways[i][j], ++cnt;
}
puts(put); //输出
四、测试运行
测试数据主要从极端数据考虑:错误输入、0处理、极限数据三个角度入手,并且自己手写了一个check函数要进行正确性的验证
check函数主要实现如下:
bool check()
{
bool col[10][10] = {false};
bool row[10][10] = {false};
bool vis[10][10] = {false};
string s = "";
rep(i,1,10) rep(j,1,10)
{
int num = a[i][j];
s += (char)(num+'0');
int t = belong[i][j];
if(vis[t][num]||col[i][num]||row[j][num]) return false;
vis[t][num] = col[i][num] = row[j][num] = true;
}
if(mp[s]) return false; //是不是输入有重复
mp[s]++;
return true;
}
N = 1
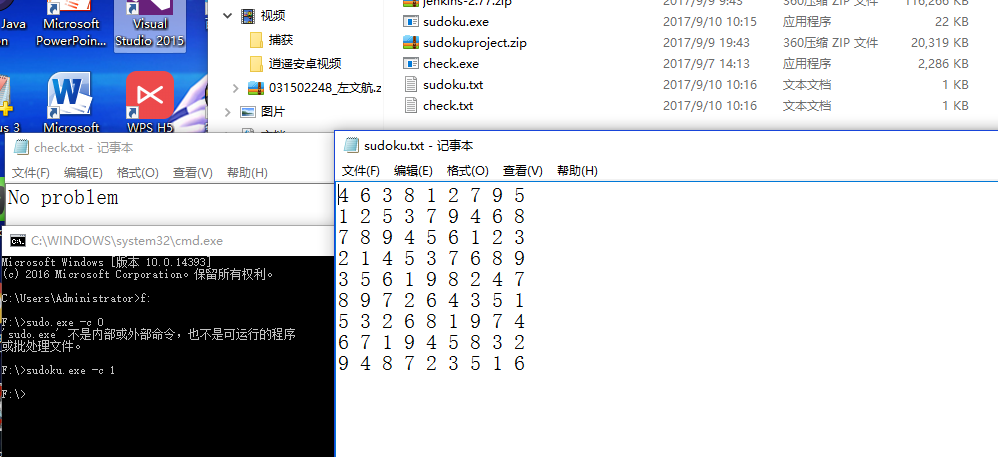
N = abc
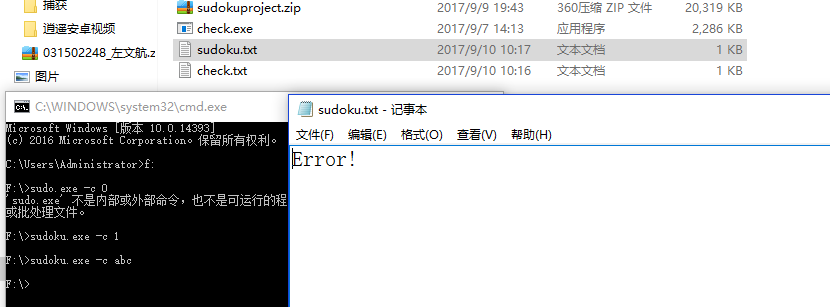
N = 1000000,注意文件输出大小
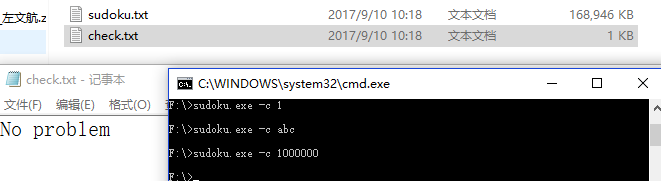
N = 0,输出为空文件
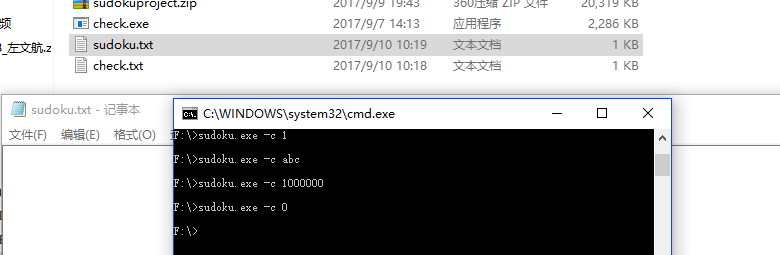
改进的过程以及性能分析
初始版本的分析
一开始的时候,我的输出是这样子的:
if(t>81)//输出方案
{
if(ans) puts(""); //两个方案之间有空格
++ans;
rep(i,1,10) rep(j,1,10)
printf("%d%c",ways[i][j],"
"[j==9]); //两个数字之间有空格
if(ans>=n) flag = true;
return ;
}
粗略自己先计算一下:
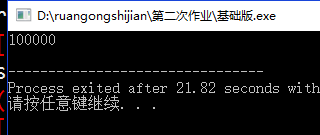
10W跑了大概20+s,难道是回溯太慢了?
写一下'换行换列'的方法:
void f(int (*a)[10])
{
int b[10] = {0,1,2,3,4,5,6,7,8,9};
do
{
if(n<=0)break;
if(flag) puts("");
else flag = true;
rep(i,1,10) rep(j,1,10)
printf("%d%c",a[i][b[j]],"
"[j==9]);
n--;
}while(next_permutation(b+1,b+10));
}
再跑一下:
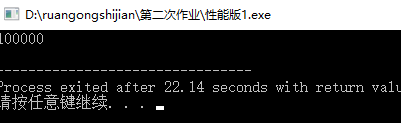
exm???还是20+s?这个就很不科学了,这个的复杂度应该很低才对啊?难道是全排列函数next_permutation跑得很慢???
于是我写了一个测试:
int a[] = {0,1,2,3,4,5,6,7,8,9};
int n;
cin >> n;
while(n--)
{
rep(i,1,10) printf("%d ",a[i]);printf("
");
next_permutation(a+1,a+10);
}
测试如下:
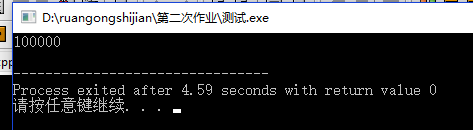
10W次的全排列居然要3、4s?这个就特别不科学了.....这个时候,我大概知道问题出在哪里了...
突然就回忆起了今年多校10的那道毒瘤题= =....1000W级别的输入,6秒的限制,卡fread才能过....
然后..我打开了vs的性能分析并且调试,这次改用N = 100W的输入


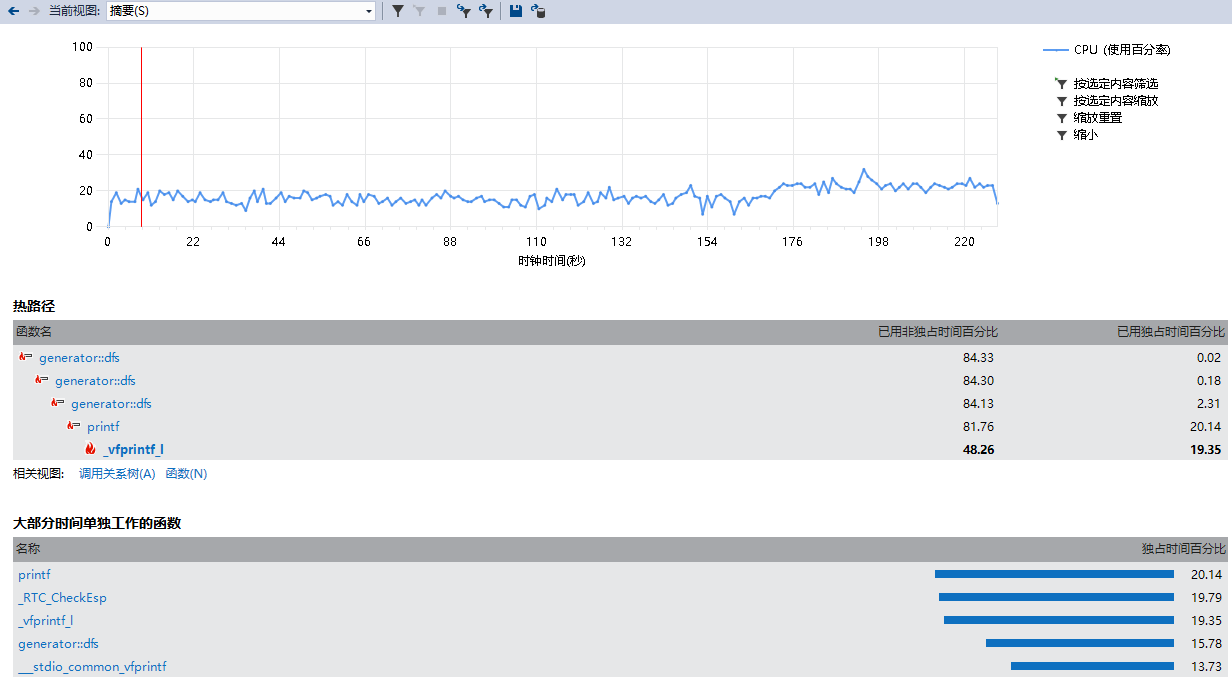
虽然我第一次弄这个性能分析,看的不是很懂,但是我还是很容易就看出来了,这几张图都指出了一个很明显的一点:printf()函数以及其的调用占了很大的时间比。

结合一下耗时,好了,该甩锅的都甩锅把,算法实际上这题占的耗时比例并不高,最大的耗时来源是在输出方式上。
改进一
于是乎,我就先用putchar()进行了二次尝试.输出由int转换为char,并且用putchar()。
if(ans) puts(""); //两个方案之间有空格
++ans;
rep(i,1,10)
{
rep(j,1,9)
putchar(ways[i][j]),putchar(' '); //两个数字之间有空格
putchar(ways[i][9]);puts("");
}
直接上100W,进行粗略估计
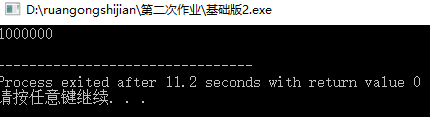
效果显著啊
改进二
然后接下来的尝试是用puts()一次性输出一个方案,即最终版本采用了这个方法。
再次直接上100W
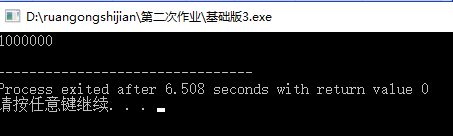
果然,更加进一步的进行了优化
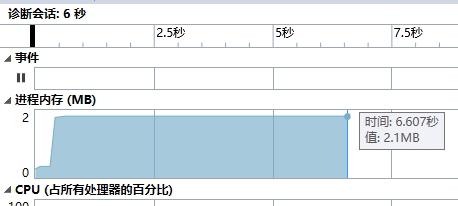
用vs性能分析查看
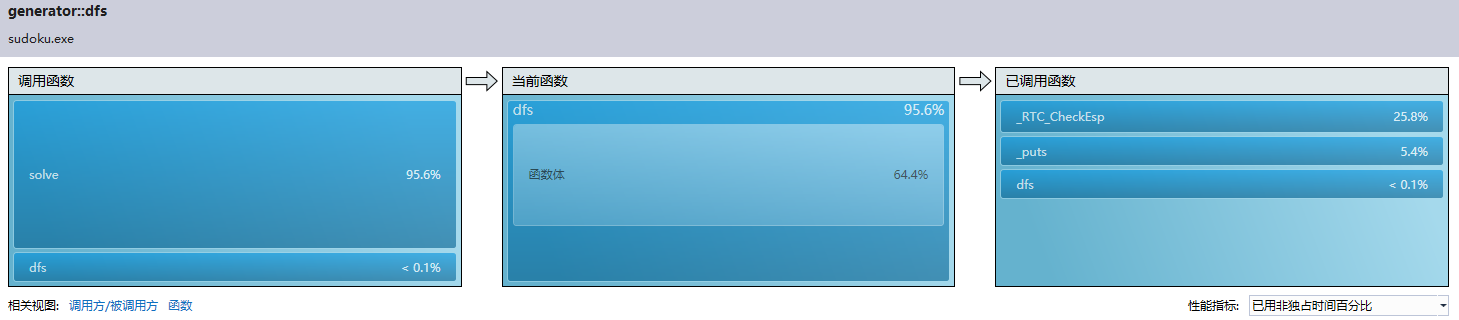
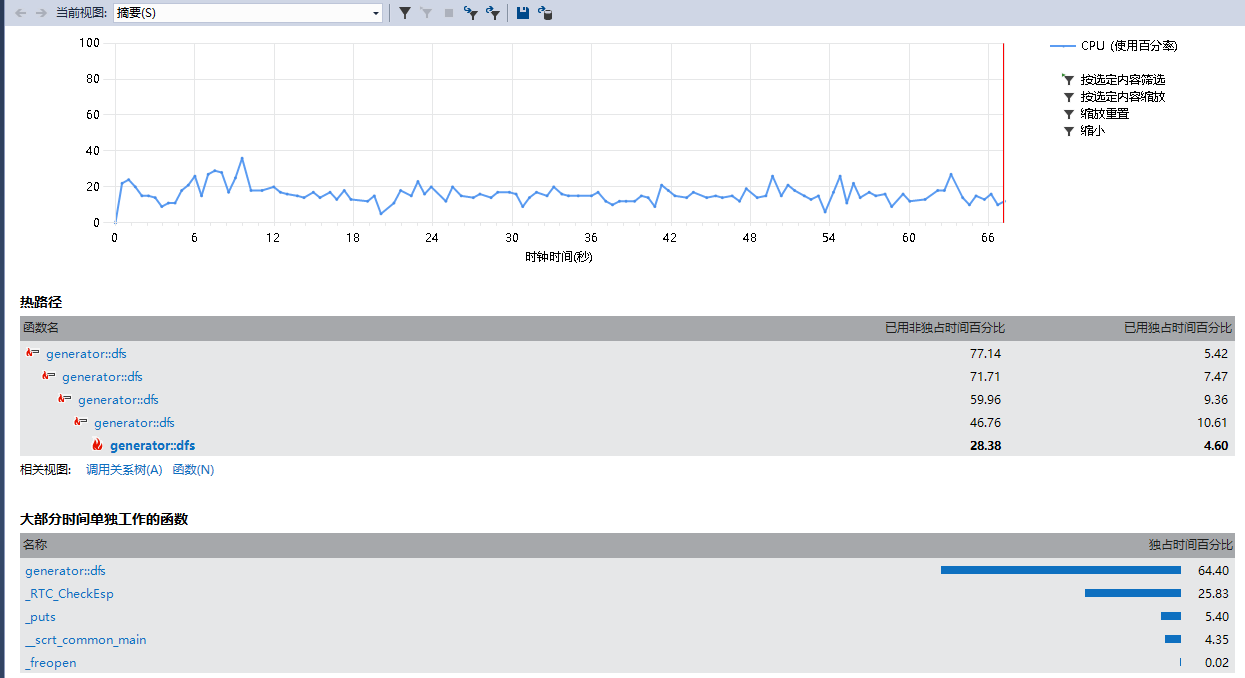
输出只占了5.8%,dfs()本身成了耗时最大的函数。
改进三
模拟缓冲区,用puts()一次性输出多个方案(附加题中使用)。
答案检查以及修改
单元测试
将自己写的check函数封装成check类,写入单元测试的项目中去,经过某犇犇的指点,得知了可以用文件的输入输出的方法,先将自己的generator类输出的答案输出到文件中去,然后再关闭输出通道,同时打开该文件的读入,这样子就可以实现check。
check主要代码如下:
bool CHECK::check(int k)
{
init();
int cas = 0;
bool f = true;
while (~scanf("%d",&a[1][1]))
{
++cas;
rep(i, 1, 10)
{
if (i == 1) rep(j, 2, 10) scanf("%d", &a[i][j]);
else rep(j, 1, 10) scanf("%d", &a[i][j]);
}
//judge用于检测生成的数独是不是正确,前面有帖写过代码
if (!judge()) f = false;
}
if (cas != k) f = false; //是不是文件中产生了k个数独
return f;
}
单元测试代码:
TEST_METHOD(TestMethod2)
{
// TODO: 在此输入测试代码
generator g;
freopen("sudoku.txt", "w", stdout);//读出文件
g.solve(10000); //生成数独
fclose(stdout); //关闭读出文件
freopen("sudoku.txt", "r", stdin);//读入文件
CHECK h;
Assert::IsTrue(h.check(10000));
}
进行测试的数据为:0、100、1000、10000、1000000,运行测试结果如下:
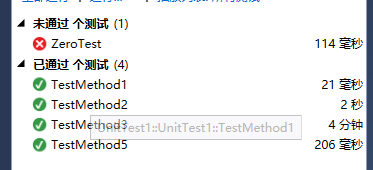
ZeroTest 未通过?查了一下,发现是因为,n = 0时,没有东西输出,这样子sudoku.txt就相当于没有刷新,保留的是上一次运行的测试的输出结果。
所以只需加一句:
if(n==0) puts("");
代码覆盖率检查
vs 2015 企业版直接使用代码覆盖率检查
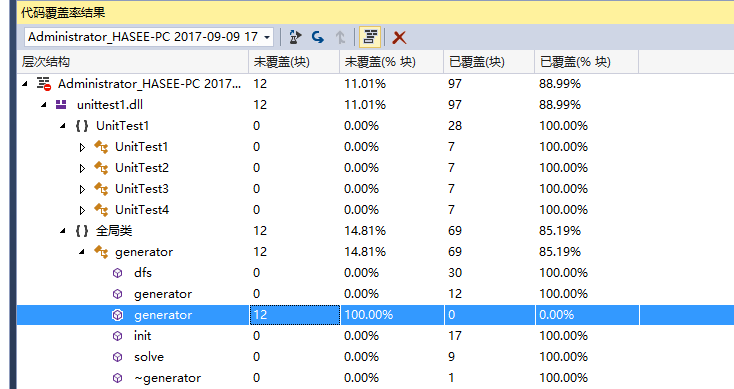
发现generator类中有未覆盖到的段,点击检查
发现是重载的构造函数未使用到,新增测试点:
generator g(5);
g.check(100);
结果如下:
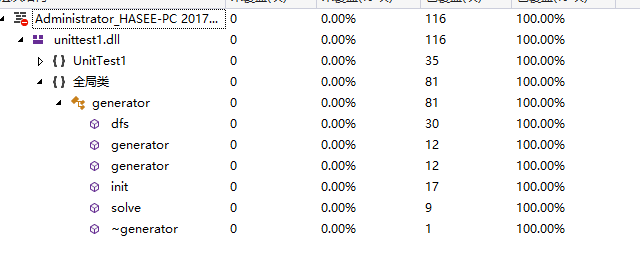

注:judge中未覆盖的片段为返回值为false时候的片段。
附加题二
随机生成N个 不重复 的 有唯一解 的数独棋盘。挖空处用数字0表示,每个数独棋盘中至少要有 30 个以上的0。输出格式见下输出示例,输出需要到文件sudoku.txt中。
解题思路**
初始版本
在第一题的基础上,每生成一个数独,就随机挖掉35个空,生成5个满足条件挖空的数独,并且每挖一次空,都进行check(查看挖掉一个空后,对该数独进行填空,查看是不是有唯一解)。
性能分析如下:

100W数据耗时大约:39s
改进版本
对初始版本进行性能分析后,发现,GetPoint()函数占用率十分的高,这个函数的作用是:**对当前数独再挖一个空,并且满足填空后数独是唯一解**
在初始版本的基础上,增加了随机函数的随机性功能,从原来的每挖一个坑就进行一个check,改成先预随机挖掉30个空,然后进行check,如果不满足条件,再重新生成30个空,之后每挖一个空,进行一次check.
100W数据大约耗时17s
最终版本
做完第二个版本后,总是在想,能不能跑的更快一点呢?突然就来了灵感,想到:如果一个数独挖了40个空是满足唯一解的,那么从中任意选31个,那么新的数独也是唯一解的,然后算一下C(40,31) = 273438880,大于100W,因此,我的做法是:
先用改进版的方法生成一个挖了40个空的数独,然后从用回溯的方法,选择挖空数大于31的数独。
100W数据大约耗时2s
遇到的困难及解决方法
没有及时的记录,因此记得不全。
1、vs使用生疏,代码分析规则不了解
问题描述
vs已经很久没有使用了,先用dev C++ 写完初稿后,一开始不知道如何在vs上创建项目,如何使用那些性能分析之类的。
dev C++的代码弄到vs上不能直接运行,如freopen会报错。
做过哪些尝试
找博客查询、找其他同学互相帮助一起解决。
是否解决
解决了,通过查询博客可以解决大部分问题.和其他同学探讨也解决了一些
有何收获
vs用更加熟悉了。
2、代码覆盖率 不知道如何下手
问题描述
vs 专业版没有代码覆盖率的功能,仔细阅读了作业要求后发现,居然,你们居然偷偷的在代码覆盖率前面加了插件两个字。
然后...我是把这个留到了最后来做的..离deadline only 2 天。
做过哪些尝试
找博客查询、找其他同学互相帮助一起解决。
1、安装插件 opencppcoverage,然后发现安装这个插件后还要安装Jenkins,然后。。Jenkins..好麻烦啊= =....我的8080端口已经有其他东西了..然后..感觉在2天之内是不可能完成的任务。
2、安装vs 2015 企业版,在舍弃了1的方案后,我决定卸载了我的vs 专业版.因为vs卸载是一件很麻烦的事情,很可能失败,但是我居然安装成功了....
是否解决
解决了。
有何收获
对代码覆盖率功能有了更深入的了解.也知道了一些开源的插件。
执行力 、 泛泛而谈 的理解
执行力我觉得是和个人的养成习惯有关,有的人有类似拖延症的毛病,做事情永远是能推迟就推迟。这就导致了,在deadline临界点,是赶工or缺交。
从某种意义上,对一件事情的重视(重要)程度,也可以在个人的执行力上体现。
也。
我习惯性的把一个大的问题分成很多个小问题,分散成很多很多个时间片去做。
其实说到底,都是意志力的问题。关键在于自己想不想做,愿不愿意花时间去做而已。
就比如..我实际上是对于作业是不拒绝的,但是我不喜欢写博客之类的.我喜欢慢慢玩,慢慢做,东西一点一点的来做,所以经常都是理论上我作业做完了,但是由于博客之类偏理论性的东西不爱做,实际上我做一件事情(完全做完)依然会拖延到很迟。
泛泛而谈,我也会这样子做,我觉得泛泛而谈有时候挺有好处的,给自己灵活变动的时间,谁都难免以外的时候突然到来,比如:今天下午我要和队友训练acm5小时,突然来了一个通知,今天下午补课,所以呢?为什么我订的目标不是:尽可能的用剩下空闲的时间就来训练。,或者说,自己发现有了更好的计划,觉得新的时间调整更加的合理,既然如此,为什么不给自己事先就预留一些灵活的使用时间,想做什么工作就做什么。
还有就是,自己本身做具体规划的时间的比较少,本身就模棱两可不知道如何规划比较好,特别是我这种有时候会较真的人,说着做2小时,突然发现某个奇怪的问题,你可能就载进去做别人看起来没有意义的事情,这样子就让时间规划变得没有意义,但是我却会觉得乐在其中.
关于经验方面的泛泛而谈,我也就不太了解,可能是出于谦虚的说话,或者本身没有什么成绩可说?一般人在介绍自己如果不是给专业人人士说的话,说一堆具体的还不如一句'经验丰富'。
不过,当然,不能全部都是泛泛而谈,因为泛泛而谈很多时候会让你缺乏执行力,结合了自身情况,我发现自己在晚自习的时候经常容易走神,为了尽可能的减少这个情况,我给自己定下了目标:一小时只能动一次手机且不能超过15min、每天晚上坚持晚自习,等等,制定具体的目标可以给人一种'紧张'或者说是'重视'的效果,让自己更加有计划,不会处于'茫然'的状态,很多人可能因为没有具体的计划就白白浪费了一天。
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 5 | 5 |
| · Estimate | · 估计这个任务需要多少时间 | 5 | 5 |
| Development | 开发 | 890 | 1020 |
| · Analysis | · 需求分析 (包括学习新技术) | 180 | 420 |
| · Design Spec | · 生成设计文档 | 120 | 90 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 60 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 120 | 30 |
| · Design | · 具体设计 | 20 | 10 |
| · Coding | · 具体编码 | 240 | 60 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 360 |
| Reporting | 报告 | 240 | 575 |
| · Test Report | · 测试报告 | 60 | 90 |
| · Size Measurement | · 计算工作量 | 10 | 5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 480 |
| 合计 | 1725 | 1600 |
|第N周 | 新增代码 (行)|累计代码(行)|本周学习耗时(小时)|累计学习耗时(小时)|重要成长|
|-------------------------|----------------|-----------------------------------------|------------------|------------------|
|0 | 1000 | 1000| 40 | 40 |vs的使用,项目创建、性能分析等|
|N | | | | |