主要内容:
- SWOMP的算法流程
- SWOMP的MATLAB实现
- 一维信号的实验与结果
- 门限参数a、测量数M与重构成功概率关系的实验与结果
- SWOMP与StOMP性能比较
一、SWOMP的算法流程
分段弱正交匹配追踪(Stagewise Weak OMP)可以说是StOMP的一种修改算法,它们的唯一不同是选择原子时的门限设置,这可以降低对测量矩阵的要求。我们称这里的原子选择方式为"弱选择"(Weak Selection),StOMP的门限设置由残差决定,这对测量矩阵(原子选择)提出了要求,而SWOMP的门限设置则对测量矩阵要求较低(原子选择相对简单、粗糙)。
SWOMP的算法流程:


二、SWOMP的MATLAB实现(CS_SWOMP.m)
function [ theta ] = CS_SWOMP( y,A,S,alpha ) % CS_SWOMP % Detailed explanation goes here % y = Phi * x % x = Psi * theta % y = Phi*Psi * theta % 令 A = Phi*Psi, 则y=A*theta % S is the maximum number of SWOMP iterations to perform % alpha is the threshold parameter % 现在已知y和A,求theta % Reference:Thomas Blumensath,Mike E. Davies.Stagewise weak gradient % pursuits[J].IEEE Transactions on Signal Processing,2009,57(11):4333-4346. if nargin < 4 alpha = 0.5; %alpha范围(0,1),默认值为0.5 end if nargin < 3 S = 10; %S默认值为10 end [y_rows,y_columns] = size(y); if y_rows<y_columns y = y'; %y should be a column vector end [M,N] = size(A); %传感矩阵A为M*N矩阵 theta = zeros(N,1); %用来存储恢复的theta(列向量) Pos_theta = []; %用来迭代过程中存储A被选择的列序号 r_n = y; %初始化残差(residual)为y for ss=1:S %最多迭代S次 product = A'*r_n; %传感矩阵A各列与残差的内积 sigma = max(abs(product)); Js = find(abs(product)>=alpha*sigma); %选出大于阈值的列 Is = union(Pos_theta,Js); %Pos_theta与Js并集 if length(Pos_theta) == length(Is) if ss==1 theta_ls = 0; %防止第1次就跳出导致theta_ls无定义 end break; %如果没有新的列被选中则跳出循环 end %At的行数要大于列数,此为最小二乘的基础(列线性无关) if length(Is)<=M Pos_theta = Is; %更新列序号集合 At = A(:,Pos_theta); %将A的这几列组成矩阵At else%At的列数大于行数,列必为线性相关的,At'*At将不可逆 if ss==1 theta_ls = 0; %防止第1次就跳出导致theta_ls无定义 end break; %跳出for循环 end %y=At*theta,以下求theta的最小二乘解(Least Square) theta_ls = (At'*At)^(-1)*At'*y; %最小二乘解 %At*theta_ls是y在At列空间上的正交投影 r_n = y - At*theta_ls; %更新残差 if norm(r_n)<1e-6 %Repeat the steps until r=0 break; %跳出for循环 end end theta(Pos_theta)=theta_ls;%恢复出的theta end
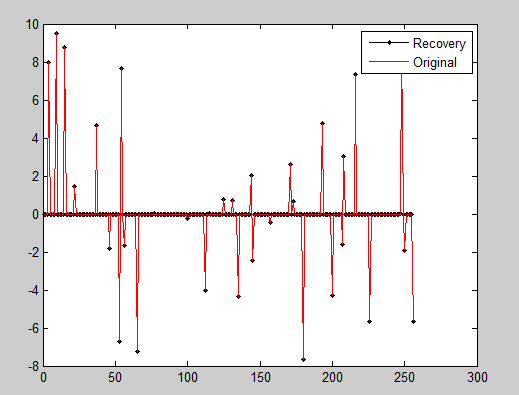
三、一维信号的实验与结果
%压缩感知重构算法测试 clear all;close all;clc; M = 128; %观测值个数 N = 256; %信号x的长度 K = 30; %信号x的稀疏度 Index_K = randperm(N); x = zeros(N,1); x(Index_K(1:K)) = 5*randn(K,1); %x为K稀疏的,且位置是随机的 Psi = eye(N); %x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta Phi = randn(M,N)/sqrt(M); %测量矩阵为高斯矩阵 A = Phi * Psi; %传感矩阵 y = Phi * x; %得到观测向量y %% 恢复重构信号x tic theta = CS_SWOMP( y,A); x_r = Psi * theta; % x=Psi * theta toc %% 绘图 figure; plot(x_r,'k.-'); %绘出x的恢复信号 hold on; plot(x,'r'); %绘出原信号x hold off; legend('Recovery','Original') fprintf(' 恢复残差:'); norm(x_r-x) %恢复残差
四、门限参数a、测量数M与重构成功概率关系的实验与结果
1、门限参数a分别为0.1-1.0时,不同稀疏信号下,测量值M与重构成功概率的关系:
clear all;close all;clc; %% 参数配置初始化 CNT = 1000; %对于每组(K,M,N),重复迭代次数 N = 256; %信号x的长度 Psi = eye(N); %x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta alpha_set = 0.1:0.1:1; K_set = [4,12,20,28,36]; %信号x的稀疏度集合 Percentage = zeros(N,length(K_set),length(alpha_set)); %存储恢复成功概率 %% 主循环,遍历每组(alpha,K,M,N) tic for tt = 1:length(alpha_set) alpha = alpha_set(tt); for kk = 1:length(K_set) K = K_set(kk); %本次稀疏度 %M没必要全部遍历,每隔5测试一个就可以了 M_set=2*K:5:N; PercentageK = zeros(1,length(M_set)); %存储此稀疏度K下不同M的恢复成功概率 for mm = 1:length(M_set) M = M_set(mm); %本次观测值个数 fprintf('alpha=%f,K=%d,M=%d ',alpha,K,M); P = 0; for cnt = 1:CNT %每个观测值个数均运行CNT次 Index_K = randperm(N); x = zeros(N,1); x(Index_K(1:K)) = 5*randn(K,1); %x为K稀疏的,且位置是随机的 Phi = randn(M,N)/sqrt(M); %测量矩阵为高斯矩阵 A = Phi * Psi; %传感矩阵 y = Phi * x; %得到观测向量y theta = CS_SWOMP(y,A,10,alpha); %恢复重构信号theta x_r = Psi * theta; % x=Psi * theta if norm(x_r-x)<1e-6 %如果残差小于1e-6则认为恢复成功 P = P + 1; end end PercentageK(mm) = P/CNT*100; %计算恢复概率 end Percentage(1:length(M_set),kk,tt) = PercentageK; end end toc save SWOMPMtoPercentage1000 %运行一次不容易,把变量全部存储下来 %% 绘图 for tt = 1:length(alpha_set) S = ['-ks';'-ko';'-kd';'-kv';'-k*']; figure; for kk = 1:length(K_set) K = K_set(kk); M_set=2*K:5:N; L_Mset = length(M_set); plot(M_set,Percentage(1:L_Mset,kk,tt),S(kk,:));%绘出x的恢复信号 hold on; end hold off; xlim([0 256]); legend('K=4','K=12','K=20','K=28','K=36'); xlabel('Number of measurements(M)'); ylabel('Percentage recovered'); title(['Percentage of input signals recovered correctly(N=256,alpha=',... num2str(alpha_set(tt)),')(Gaussian)']); end for kk = 1:length(K_set) K = K_set(kk); M_set=2*K:5:N; L_Mset = length(M_set); S = ['-ks';'-ko';'-kd';'-k*';'-k+';'-kx';'-kv';'-k^';'-k<';'-k>']; figure; for tt = 1:length(alpha_set) plot(M_set,Percentage(1:L_Mset,kk,tt),S(tt,:));%绘出x的恢复信号 hold on; end hold off; xlim([0 256]); legend('alpha=0.1','alpha=0.2','alpha=0.3','alpha=0.4','alpha=0.5',... 'alpha=0.6','alpha=0.7','alpha=0.8','alpha=0.9','alpha=1.0'); xlabel('Number of measurements(M)'); ylabel('Percentage recovered'); title(['Percentage of input signals recovered correctly(N=256,K=',... num2str(K),')(Gaussian)']); end
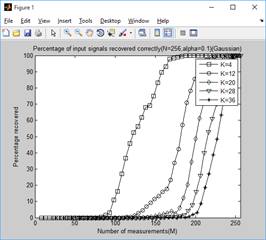
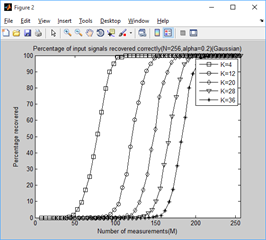
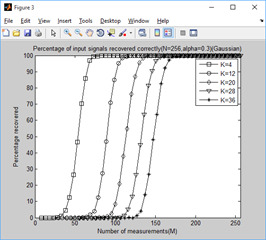

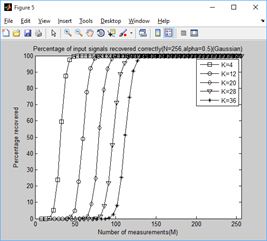
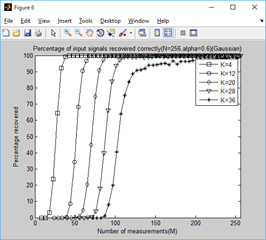
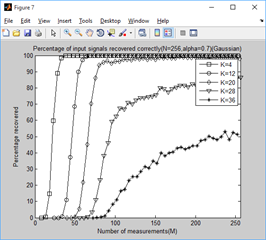
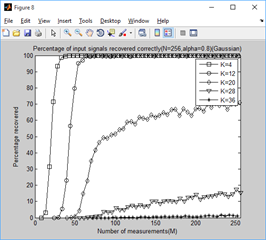
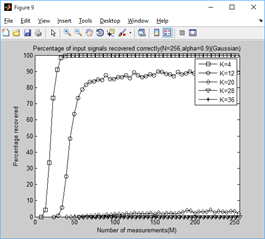
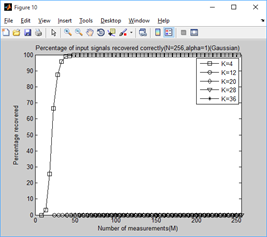
2、稀疏度为4,12,20,28,36时,不同门限参数a下,测量值M与重构成功概率的关系:
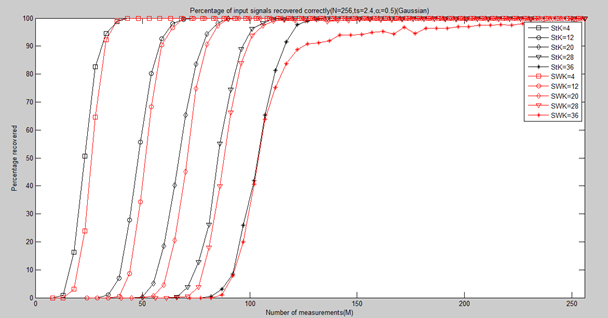
clear all;close all;clc; load StOMPMtoPercentage1000; PercentageStOMP = Percentage; S = ['-ks';'-ko';'-kd';'-kv';'-k*']; figure; for kk = 1:length(K_set) K = K_set(kk); M_set=2*K:5:N; L_Mset = length(M_set); %ts_set = 2:0.2:3;第3个为2.4 plot(M_set,Percentage(1:L_Mset,kk,3),S(kk,:));%绘出x的恢复信号 hold on; end load SWOMPMtoPercentage1000; PercentageSWOMP = Percentage; S = ['-rs';'-ro';'-rd';'-rv';'-r*']; for kk = 1:length(K_set) K = K_set(kk); M_set=2*K:5:N; L_Mset = length(M_set); %alpha_set = 0.1:0.1:1;第6个为0.6 plot(M_set,Percentage(1:L_Mset,kk,6),S(kk,:));%绘出x的恢复信号 hold on; end hold off; xlim([0 256]); legend('StK=4','StK=12','StK=20','StK=28','StK=36',... 'SWK=4','SWK=12','SWK=20','SWK=28','SWK=36'); xlabel('Number of measurements(M)'); ylabel('Percentage recovered'); title(['Percentage of input signals recovered correctly(N=256,ts=2.4,alpha=0.5)(Gaussian)']);
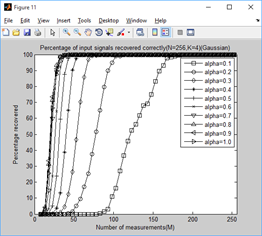
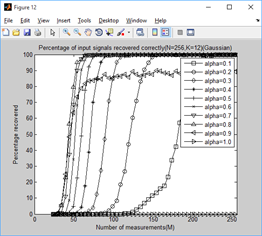
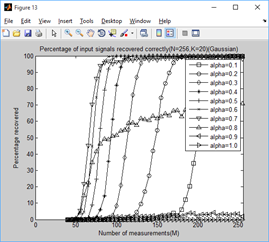
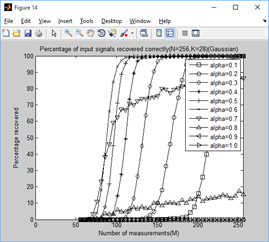
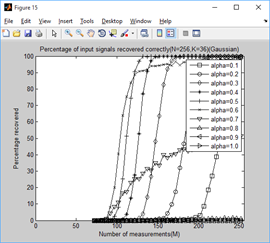
结论:
通过对比可以看出,总体上讲a=0.6时效果较好。
五、SWOMP与StOMP性能比较
对比StOMP中ts=2.4与SWOMP中α=0.6的情况:StOMP要略好于SWOMP。