Maxima 使用教程

说起数学软件，我们很多人脑子里浮现出的第一个就是 matlab，不可否认，matlab 确实是一个优秀的数学软件，但是它需要付费啊（这里不讨论盗版问题）。那么有没有一个同样强大但免费的数学软件呢？答案是肯定的，那就是本文所要说的 Maxima，当然了，不只是有这一个。

预备知识

在正式介绍其使用方法之前，想先介绍 Maxima 里面一些规则。

1. 在求极限的时候，如果极限不存在，范围值可能为 und（极限不存在），ind（极限不存在但是有界），infinity（发散）
2. 自然常数 e 用 %e 表示
3. 圆周率 π 用 %pi 表示
4. 注释：方法与 C 语言相同，/*...*/

一、求极限

在 Maxima 中用 limit 函数来进行极限求解。

limit (expr, x, val)  /*计算 x 趋近于 val 时 expr 的极限*/

limit (expr, x, val, dir) /*dir 为 plus 时求的是右极限，为 minus 时求的是左极限。*/

例如：

limit(sin(x)/x,x,0);

limit((1+1/x)^x,x,inf);

limit((2^(1/x)+1)/(2^(1/x)-1),x,0);

limit((2^(1/x)+1)/(2^(1/x)-1),x,0,minus);

limit((2^(1/x)+1)/(2^(1/x)-1),x,0,plus);

limit((2*x^2+x)/(x^2-2),x,inf);

二、求和与求积运算

可以使用 sum 和 product 函数进行求和以及求积操作。

sum (expr, i, i_0, i_1)  /*求和*/
product (expr, i, i_0, i_1) /*求积*/

例如：

sum (i^2, i, 1, 7);

sum (a[i], i, 1, 7);

sum(1/k^2,k,0,inf);

sum (1/3^i, i, 1, inf), simpsum;

product (x + i*(i+1)/2, i, 1, 4);

product (a(i), i, 1, n);

product (k, k, 1, n), simpproduct;

三、taylor 级数展开

函数f(x)的在 x = a 附近的幂级数可以通过 powerseries (f(x), x, a) 获得。

powerseries (f(x), x, a);/*求 x=a 处f(x)的幂级数*/

例如：

powerseries(1/(1-x^2), x, 0);

 

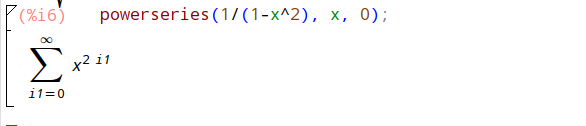
上面得到的结果中的求和指数 i2 看起来显得不那么专业，可以用 niceindices 函数将其变的看起来更专业些。

niceindices(powerseries(1/(1-x^2), x, 0));

很多时候我们无法得到级数的解析表示，这时候可以用 taylor (f(x), x, a, n)得到函数f(x)在x = a附近第 n 阶项（(x - a)^n）以下各项的泰勒级数

taylor(sin(x), x, 0, 8);

同样，对多元函数也可以进行 taylor 展开。

taylor (sin (y + x), x, 0, 3, y, 0, 3);

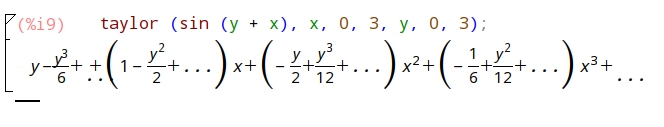
利用 pade 近似可以将 taylor 级数转化为多项式函数。比如下面的例子

taylor(sin(x), x, 0, 8);

pade(%,5,5);

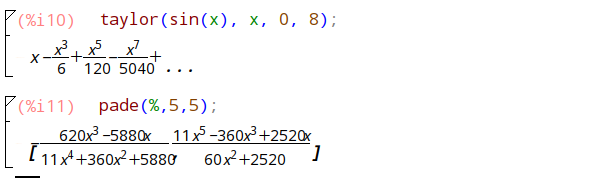
未完待续！！

作者：耑新新，发布于  博客园

转载请注明出处，欢迎邮件交流：zhuanxinxin@aliyun.com