树与森林
1. 什么是森林
森林,顾名思义,就是由众多的树构成的一组数据结构,这些树本身没有什么联系,用系统的语言描述就是:森林:m(>=0)棵互不相交的树的集合 【注意这里森林是可以有0颗树的,同数学上的空集】
如果把一棵树当作一个独立的点,那么森林就是一个点的集合。
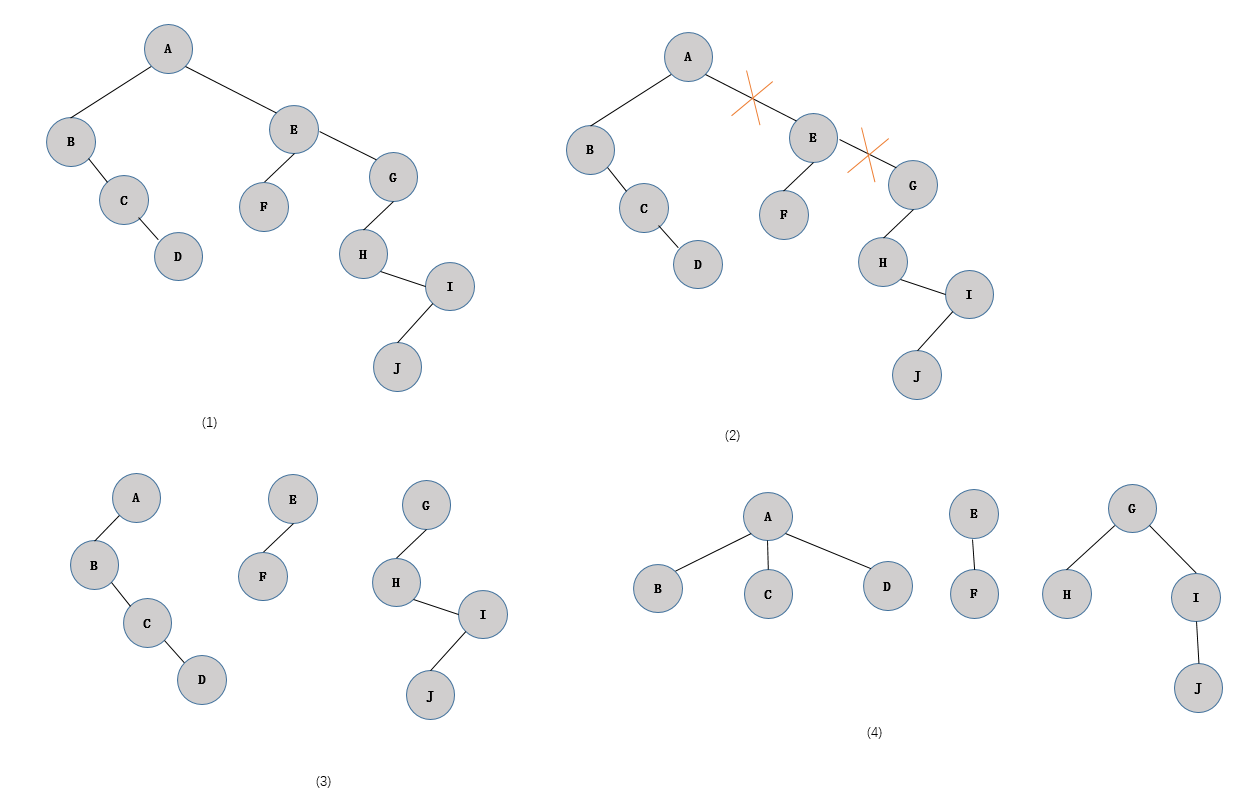
2. 树转换成二叉树
操作过程如下:
加线:在兄弟(即同一层之间的孩子)之间加一连线
抹线:对每个结点,除了其第一个孩子外,除去其与其余孩子之间的连线
旋转:以树的根结点为轴心,将整树顺时针转45°
如图:
注意:树转换成二叉树其右子树一定为空
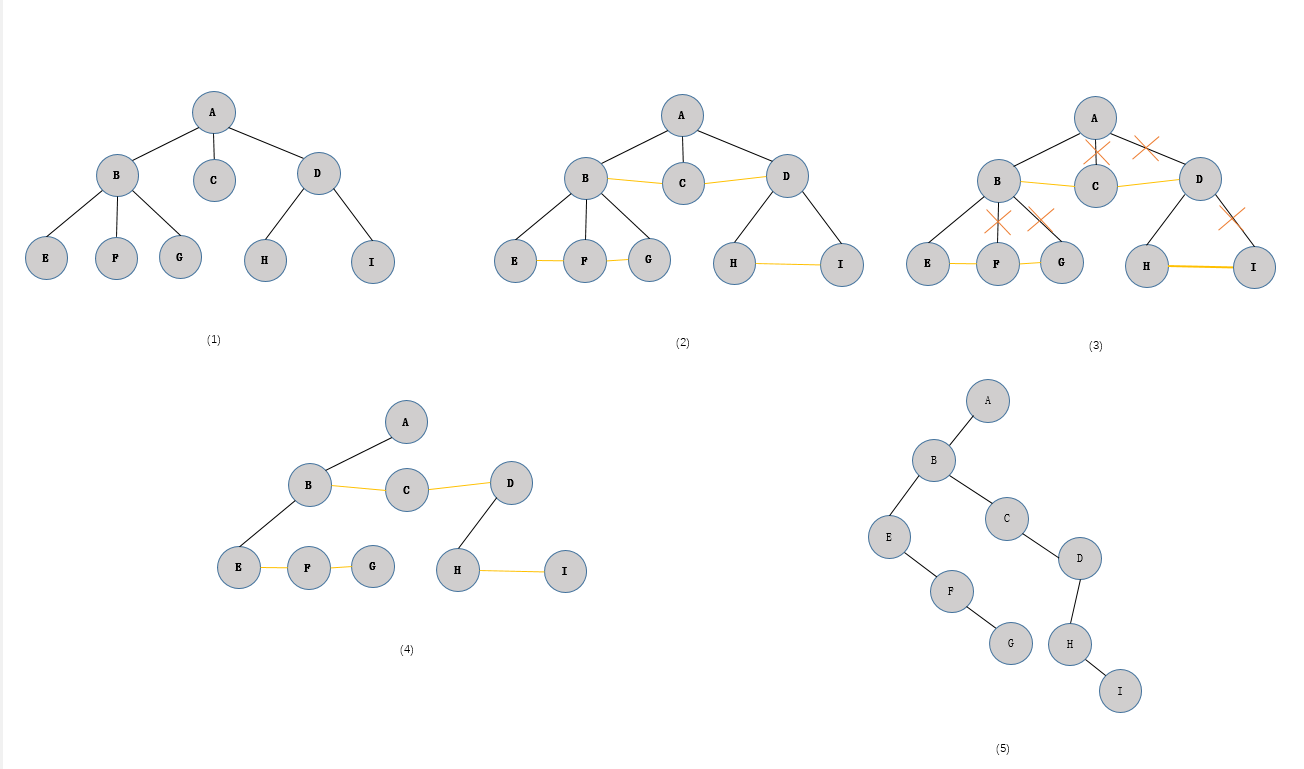
3. 二叉树转换成树
加线:若p结点是双亲结点的左孩子,则将p的右孩子,右孩子的右孩子,……沿分支找到的所有右孩子,都与p的双亲用线连起来
抹线:抹掉原二叉树中双亲与右孩子之间的连线
调整:将结点按层次排列,形成树结构
如图:
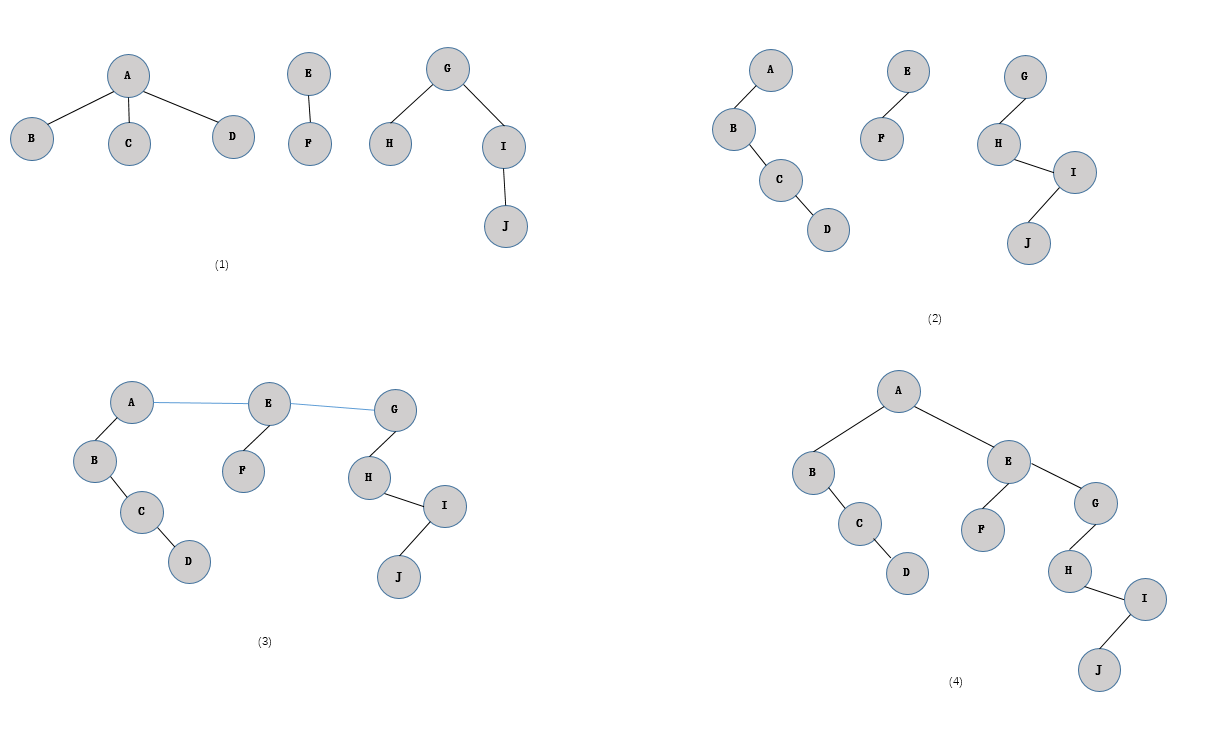
4. 森林转换成二叉树
将各棵树分别转换成二叉树
将每棵树的根结点用线相连
以第一棵树根结点为二叉树的根,再以根结点为轴心,顺时针旋转,构成二叉树型结构
如图:
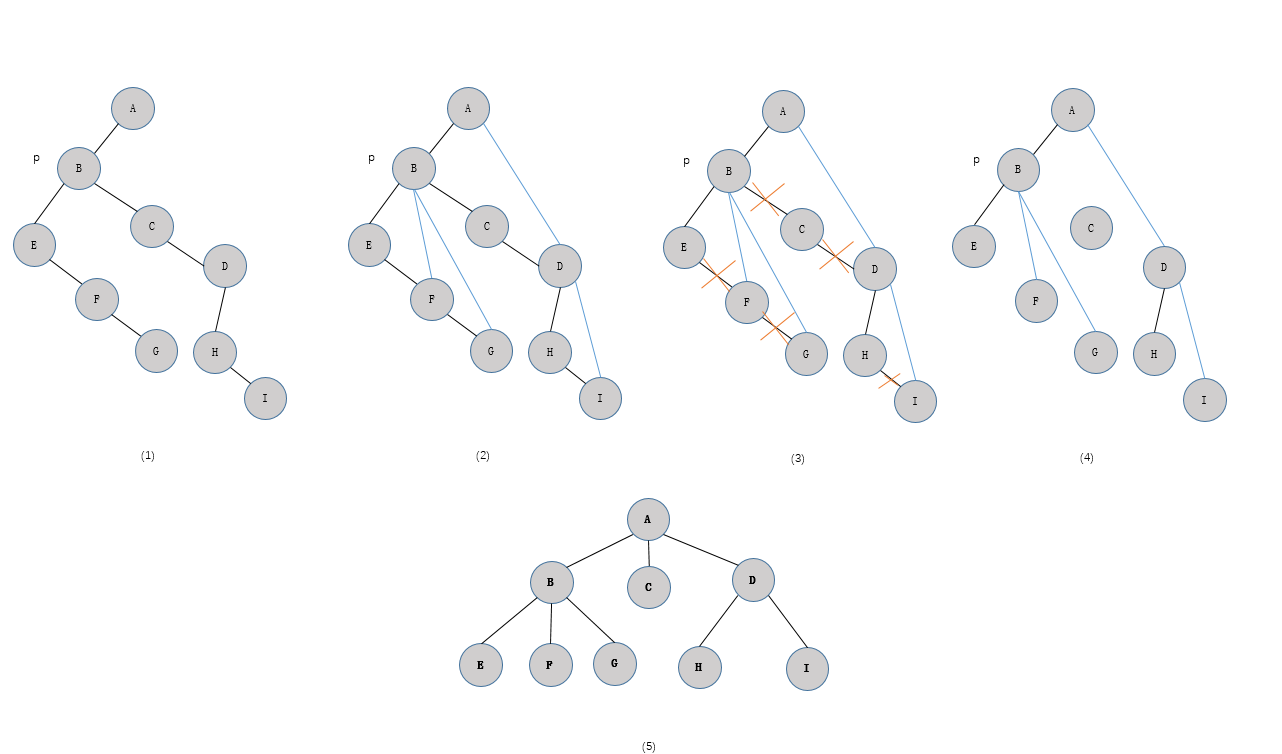
5. 二叉树转换成森林
抹线:将二叉树中根结点与其右孩子连线,及沿右分支搜索到的所有右孩子间连线全部抹掉,使之变成孤立的二叉树
还原:将孤立的二叉树还原成树(二叉树→树)
如图: