前言
斜率优化通常使用单调队列辅助进行实现,用于优化 (DP) 的时间复杂度。
适用范围
使用单调队列优化 (DP) ,通常可以解决型如: (dp[i]=min(f(j))+g(i)) 的状态转移方程。其中 (f(i)) 是只关于 (i) 的函数, (g(j)) 是只关于 (j) 的函数。朴素的解决方法是在第二层循环中枚举 (j) 来实现最小值,时间复杂度为 (O(n^2)) 。可以使用单调队列来维护这个最小值实现 (O(n)) 的时间复杂度。
而斜率优化利用上述方法进行改进,实现对于型如: (dp[i]=min(f(i,j))+g(i)) 的状态转移方程。对比第一种情况,可以发现函数 (f) 函数与两个值 (i,j) 都有关,简单地使用单调队列是无法优化的。这时候就开始引入主题斜率优化了。
下面结合一道例题来具体详解。题目来自于 (HNOI2008) 省选题目。
题目大意
有 (n) 个数字 (C_1) , (C_2...C_n) ,把它分为若干组,给出另一个数 (L) ,设每组的第一个数下标为 (i) ,最后一个数下标为 (j) ,则每组的花费为((i-j+sum_{k=i}^jC_k-L)^2),总花费为所有组的花费之和。求最小总花费。
思路
先考虑朴素的 (dp) 做法。
设 (dp[i]) 为将前 (i) 个数字分组后的最小花费。求和可以考虑使用前缀和来优化,设前缀和数组为 (pre) 。则状态转移方程可以写为:
(dp[i]=Min(dp[j]+(sum[i]-sum[j])+(i-(j+1))-L)^2,0≤j<i))
即是:
(dp[i]=Min(dp[j]+(sum[i]-sum[j]+i-j-L-1)^2,0≤j<i))
那么 (sum) 数组可以初始化为:
for(int i = 1; i <= n; i++) {
Quick_Read(val[i]);
sum[i] = sum[i - 1] + val[i];
}
设 (pre[i]=sum[i]+i) ,再进一步设 (l=L+1) 那么状态转移方程可以写为:
(dp[i]=Min(dp[j]+(pre[i]-pre[j]-l)^2,0≤j<i))
状态转移
int Get_Dp(int i, int j) {
return dp[j] + (pre[i] - pre[j] - l) * (pre[i] - pre[j] - l);
}
(pre) 数组就可以进一步写为:
for(int i = 1; i <= n; i++) {
Quick_Read(val[i]);
pre[i] = pre[i - 1] + val[i] + 1;
}
若枚举 (j) ,则时间复杂度为 (O(n)^2) ,时间复杂度不优。使用斜率优化可以对其进行优化。
假设当前枚举到 (i) ,需要得到 (i) 的状态。假设有两个决策点 (j) , (k) ,满足决策点 (j) 优于决策点 (k) 。用符号语言可以表达为:
(dp[j]+(pre[i]-pre[j]-l)^2<dp[k]+(pre[i]-pre[k]-l)^2)
展开得:
(dp[j]+pre[i]^2+pre[j]^2+l^2-2 imes pre[i] imes pre[j]-2 imes l imes pre[i]+2 imes l imes pre[j]<dp[k]+pre[i]^2+pre[k]^2+l^2-2 imes pre[i] imes pre[k]-2 imes l imes pre[i]+2 imes l imes pre[k])
进一步整理得 :
(dp[j]+pre[j]^2-dp[k]-pre[k]^2<(pre[i]-l) imes 2 imes (pre[j] - pre[k]))
观察可得:左边的式子只与 (j) 和 (k) 有关,但右边的式子还与 (i) 有关。也可以发现若满足上述式子,则会有 (j) 优于 (k) 。再分类讨论:
- (j>k) ,则 (pre[j]>pre[k]),移项得 (frac{dp[j]+pre[j]^2-(dp[k]+pre[k]^2)}{pre[j] - pre[k]}<pre[i]-l) , (2 imes (pre[i]-l)) 可以 看为一个常数。那么意味着点 (j(dp[j]+pre[j]^2,pre[j])) 与点 (k(dp[k]+pre[k]^2,pre[k])) 所构成的直线的斜率小于 (2 imes (pre[i]-l)) 这个常数。
- (j<k) ,则 (pre[j]<pre[k]),移项得 (frac{dp[j]+pre[j]^2-(dp[k]+pre[k]^2)}{pre[j] - pre[k]}>pre[i]-l) , (2 imes (pre[i]-l)) 可以 看为一个常数。那么意味着点 (j(dp[j]+pre[j]^2,pre[j])) 与点 (k(dp[k]+pre[k]^2,pre[k])) 所构成的直线的斜率大于 (2 imes (pre[i]-l)) 这个常数。
获得分子的函数:
int Get_Up(int j, int k) {
return dp[j] + pre[j] * pre[j] - dp[k] - pre[k] * pre[k];
}
获得分母的函数:
int Get_Down(int j, int k) {
return pre[j] - pre[k];
}
有了上述的一级结论,可以进一步推导出二级结论:
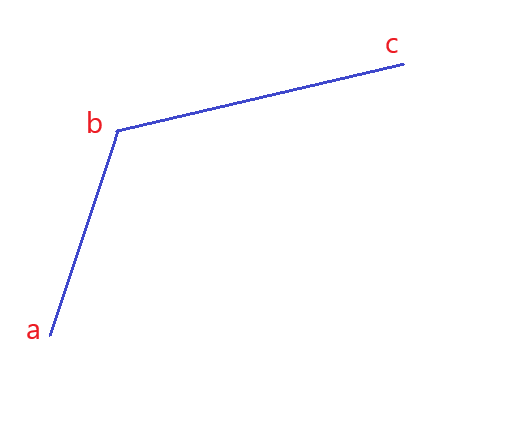
设 (x,y) 的斜率表示为 (k(x,y)) 。若存在三点 (a,b,c) ,有 (k(a,b)>k(b,c)) ,即是图像形成上凸的形状时,那么点 (b) 绝对不是最优的。
分类讨论:
- (k(a,b)>k(b,c)>pre[i]-l) ,则对于上述结论可以得出 (a) 比 (b) 更优,舍去 (b) 。
- (pre[i]-l>k(a,b)>k(b,c)) ,则对于上述结论可以得出 (c) 比 (b) 更优,舍去 (b) 。
- (pre[i]-l<k(a,b)) 且 (pre[i]-l>k(b,c)) ,则对于上述结论可以得出 (a) 和 (c) 都比 (b) 更优,舍去 (b) 。
那么就可以得出答案的点必须满足 (k(a_1,a_2)<k(a_2,a_3)<...<k(a_{m-1},a_m)) 。全部呈现出下凸状态,如下图。
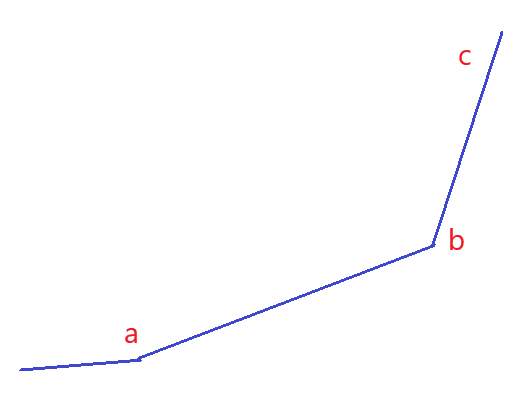
这样下标递增,斜率递增的点集可以使用单调队列来维护。
找出当前最优的点为 (que[head]) ,即队头元素。
while(Get_Up(que[head + 1], que[head]) <= 2 * (pre[i] - l) * Get_Down(que[head + 1], que[head]) && head < tail)
head++;
用当前点 (i) 来更新队列,使得该队列呈下凸之势。
while(Get_Up(que[tail], que[tail - 1]) * Get_Down(i, que[tail]) >= Get_Up(i, que[tail]) * Get_Down(que[tail], que[tail - 1]) && head < tail)
tail--;
按照上述方法进行状态转移,得到的 (dp[n]) 就是当前的最优解。
C++代码
注意要开 (long) (long)
#include <cstdio>
#define int long long//注意开long long吖( ⊙ o ⊙ )!
void Quick_Read(int &N) {//快速读入
N = 0;
int op = 1;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-')
op = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
N = (N << 1) + (N << 3) + (c ^ 48);
c = getchar();
}
N *= op;
}
void Quick_Write(int N) {//快速打印
if(N < 0) {
putchar('-');
N = -N;
}
if(N >= 10)
Quick_Write(N / 10);
putchar(N % 10 + 48);
}
const int MAXN = 5e5 + 5;
int dp[MAXN];
int pre[MAXN], val[MAXN];
int n, l;
int que[MAXN];
int head, tail;
int Get_Dp(int i, int j) {//状态转移方程
return dp[j] + (pre[i] - pre[j] - l) * (pre[i] - pre[j] - l);
}
int Get_Up(int j, int k) {//获得斜率的分子
return dp[j] + pre[j] * pre[j] - dp[k] - pre[k] * pre[k];
}
int Get_Down(int j, int k) {//获得斜率的分母
return pre[j] - pre[k];
}
void Line_Dp() {
head = 1;//单调队列初始化,dp[0]也是一种方案,所以头和尾都是1
tail = 1;
for(int i = 1; i <= n; i++) {
while(Get_Up(que[head + 1], que[head]) <= 2 * (pre[i] - l) * Get_Down(que[head + 1], que[head]) && head < tail)
head++;//找到当前的最优解
dp[i] = Get_Dp(i, que[head]);//状态转移
while(Get_Up(que[tail], que[tail - 1]) * Get_Down(i, que[tail]) >= Get_Up(i, que[tail]) * Get_Down(que[tail], que[tail - 1]) && head < tail)
tail--;//把i加入单调队列更新最优解
que[++tail] = i;
}
Quick_Write(dp[n]);//输出答案
}
void Read() {//输入数据
Quick_Read(n);
Quick_Read(l);
l++;
for(int i = 1; i <= n; i++) {
Quick_Read(val[i]);
pre[i] = pre[i - 1] + val[i] + 1;
}
}
signed main() {
Read();
Line_Dp();
return 0;
}