[AGC005C]Tree Restoring 构造

Description

​ 给出一个数组a,要求构造一颗树，使节点x距离最远的点的距离为(a_x)。

Input

​ 第一行一个正整数NN（2≤N≤1002≤N≤100）

​ 接下来一行，有NN个正整数，描述序列a1,a2,...,aNa1,a2,...,aN（1≤ai≤N−11≤ai≤N−1）

Output

​ 如果对于输入的序列存在这样的树，则输出"Possible"，否则输出"Impossible"。二者皆不含引号。

Sample Input

#Sample Input 1
5
3 2 2 3 3

#Sample Input 2
3
1 1 2

#Sample Input 3
10
1 2 2 2 2 2 2 2 2 2

#Sample Input 4
10
1 1 2 2 2 2 2 2 2 2

#Sample Input 5
6
1 1 1 1 1 5

#Sample Input 6
5
4 3 2 3 4

Sample Output

#Sample Output 1
Possible

#Sample Output 2
Impossible

#Sample Output 3
Possible

#Sample Output 4
Impossible

#Sample Output 5
Impossible

#Sample Output 6
Possible

HINT

​ 对于第一组样例，有如下美妙树：

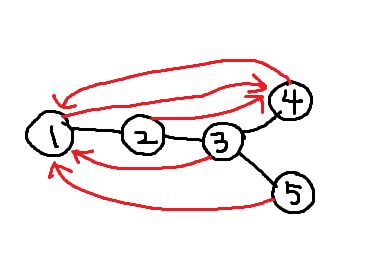
​ 黑边表示原树边，而红边表示的是距离每一个点最远的点是谁。

Sol

显然只要能把直径构造出来，那么剩下的点无论如何也能构造出来，首先判断最小的(a_i)能否达到(直径长度lceilfrac{直径长度}{2} ceil)，然后我们枚举直径长度到(直径长度lceilfrac{直径长度}{2} ceil)的所有长度，如果不到两个那么就不可行，否则可行。注意如果直径长度是偶数的话(直径长度lceilfrac{直径长度}{2} ceil)有一个就可以了。

Code

#include <bits/stdc++.h>
using namespace std;
int a[105],b[105],n,mid,g;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[a[i]]++;
    sort(a+1,a+n+1,greater<int>());mid=(a[1]+1)>>1,g=(a[1]&1)+1;
    if(a[n]<mid||b[mid]!=g) return puts("Impossible"),0;
    for(int i=a[1];i>mid;i--) if(b[i]<2) return puts("Impossible"),0;
    puts("Possible");
}