1 #include <cstdio>
2 #define ll long long
3 using namespace std;
4 const ll N=5010,mo=1e9+7;
5 struct edge { int to,from; }e[N*2];
6 ll f[N][N][2],head[N],size[N],jc[N],g[N],ans,n,cnt,r;
7 void insert(int x,int y) { e[++cnt].to=y,e[cnt].from=head[x],head[x]=cnt; }
8 ll ksm(ll a,ll b){ for (r=1;b;b>>=1,a=a*a%mo) if (b&1) r=r*a%mo; return r;}
9 ll C(ll x,ll y) { return jc[y]*ksm(jc[y-x],mo-2)%mo*ksm(jc[x],mo-2)%mo; }
10 void dfs(int d,int x,int y,int l,int r)
11 {
12 if (d>g[0]) { (f[x][r][l]+=y)%=mo; return; }
13 for (int i=0;i<=size[g[d]];i++) if (f[g[d]][i][l]) dfs(d+1,x,y*f[g[d]][i][l]%mo,l,r+i);
14 }
15 void dp(int x,int y,int k)
16 {
17 for (int i=head[x];i;i=e[i].from) if (e[i].to!=y) dp(e[i].to,x,k^1),size[x]+=size[e[i].to];
18 g[0]=0; for (int i=head[x];i;i=e[i].from) if (e[i].to!=y) g[++g[0]]=e[i].to;
19 if (size[x])
20 {
21 dfs(1,x,1,k,0);
22 for (int i=0;i<=size[x];i++) f[x][i][k^1]=(C(i,size[x])-f[x][i][k]+mo)%mo;
23 }
24 else size[x]++,f[x][0][0]=f[x][1][1]=1;
25 }
26 int main()
27 {
28 freopen("game.in","r",stdin),freopen("game.out","w",stdout),scanf("%lld",&n);
29 for (int i=1,x,y;i<n;i++) scanf("%d%d",&x,&y),insert(x,y),insert(y,x);
30 jc[0]=1; for (int i=1;i<=n;i++) jc[i]=jc[i-1]*i%mo; dp(1,0,0);
31 for (int i=0;i<=size[1];i++) (ans+=f[1][i][1]*jc[i]%mo*jc[size[1]-i]%mo)%=mo;
32 printf("%lld",ans);
33 }
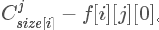 。对于偶层,也就是小B取值也是一样的
。对于偶层,也就是小B取值也是一样的