BUAA_OO_博客作业一

BUAA_OO_博客作业一

（一）程序结构分析

1.代码统计

第一次作业

第二次作业

第三次作业

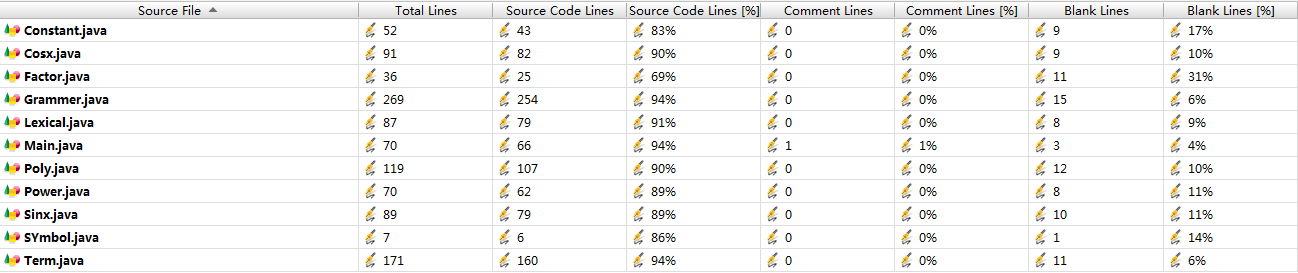
代码复杂度展示第三次作业的

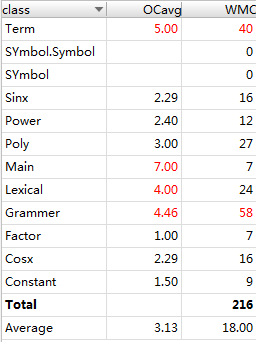
method	ev(G)	iv(G)	v(G)
Constant.Constant(BigInteger)	1.0	1.0	1.0
Constant.derv()	1.0	1.0	1.0
Constant.mul(ArrayList)	4.0	5.0	5.0
Constant.mul(BigInteger)	1.0	1.0	1.0
Constant.mul(Constant)	1.0	1.0	1.0
Constant.toString()	1.0	1.0	1.0
Cosx.Cosx(BigInteger,Factor)	1.0	1.0	1.0
Cosx.derv()	2.0	2.0	3.0
Cosx.equal(Cosx)	2.0	1.0	2.0
Cosx.isEqual(Cosx)	2.0	1.0	2.0
Cosx.mul(ArrayList)	4.0	4.0	4.0
Cosx.mul(Cosx)	1.0	1.0	1.0
Cosx.toString()	3.0	3.0	3.0
Factor.derv()	1.0	1.0	1.0
Factor.mul(ArrayList)	1.0	1.0	1.0
Factor.mul(Constant)	1.0	1.0	1.0
Factor.mul(Cosx)	1.0	1.0	1.0
Factor.mul(Power)	1.0	1.0	1.0
Factor.mul(Sinx)	1.0	1.0	1.0
Factor.toString()	1.0	1.0	1.0
Grammer.analyze()	3.0	4.0	8.0
Grammer.deleteop(String)	1.0	1.0	1.0
Grammer.getconstant(Symbol)	2.0	5.0	5.0
Grammer.getcosx(Symbol)	4.0	3.0	4.0
Grammer.getdeg()	5.0	4.0	6.0
Grammer.getfactor(Symbol)	2.0	2.0	9.0
Grammer.getpoly()	4.0	4.0	8.0
Grammer.getpolyfactor(Symbol)	3.0	2.0	3.0
Grammer.getpower(Symbol)	2.0	1.0	2.0
Grammer.getsinx(Symbol)	4.0	3.0	4.0
Grammer.getterm(Symbol)	4.0	4.0	6.0
Grammer.Grammer(String)	1.0	1.0	1.0
Grammer.wf()	1.0	1.0	1.0
Lexical.back()	1.0	1.0	1.0
Lexical.getnum()	1.0	1.0	1.0
Lexical.getword()	16.0	7.0	21.0
Lexical.instr()	1.0	1.0	1.0
Lexical.Lexical(String)	1.0	1.0	1.0
Lexical.wf()	1.0	1.0	1.0
Main.main(String[])	1.0	8.0	8.0
Poly.add(Term)	4.0	5.0	5.0
Poly.derv()	1.0	2.0	2.0
Poly.getarray()	1.0	1.0	1.0
Poly.isEmpty()	1.0	1.0	1.0
Poly.mul(ArrayList)	1.0	1.0	1.0
Poly.opt()	1.0	7.0	7.0
Poly.opt2()	1.0	6.0	6.0
Poly.Poly()	1.0	1.0	1.0
Poly.toString()	2.0	3.0	4.0
Power.derv()	2.0	3.0	3.0
Power.mul(ArrayList)	4.0	4.0	4.0
Power.mul(Power)	1.0	1.0	1.0
Power.Power(BigInteger)	1.0	1.0	1.0
Power.toString()	3.0	3.0	3.0
Sinx.derv()	2.0	2.0	3.0
Sinx.equal(Sinx)	2.0	1.0	2.0
Sinx.isEqual(Sinx)	2.0	1.0	2.0
Sinx.mul(ArrayList)	4.0	4.0	4.0
Sinx.mul(Sinx)	1.0	1.0	1.0
Sinx.Sinx(BigInteger,Factor)	1.0	1.0	1.0
Sinx.toString()	3.0	3.0	3.0
Term.add(Factor)	6.0	10.0	12.0
Term.derv()	3.0	2.0	3.0
Term.getterm()	1.0	1.0	1.0
Term.insert(char)	6.0	6.0	6.0
Term.isEqual(Term)	2.0	2.0	3.0
Term.opt()	10.0	20.0	23.0
Term.Term()	1.0	1.0	1.0
Term.toString()	2.0	2.0	4.0
Total	159.0	181.0	234.0
Average	2.3043478260869565	2.6231884057971016	3.391304347826087

### **2.代码结构图**

以我第三次作业的程序结构进行分析（结构图包括各个类的成员变量和方法以及类之间的关系）

![](https://img2018.cnblogs.com/blog/1616145/201903/1616145-20190323232339188-898216720.png)

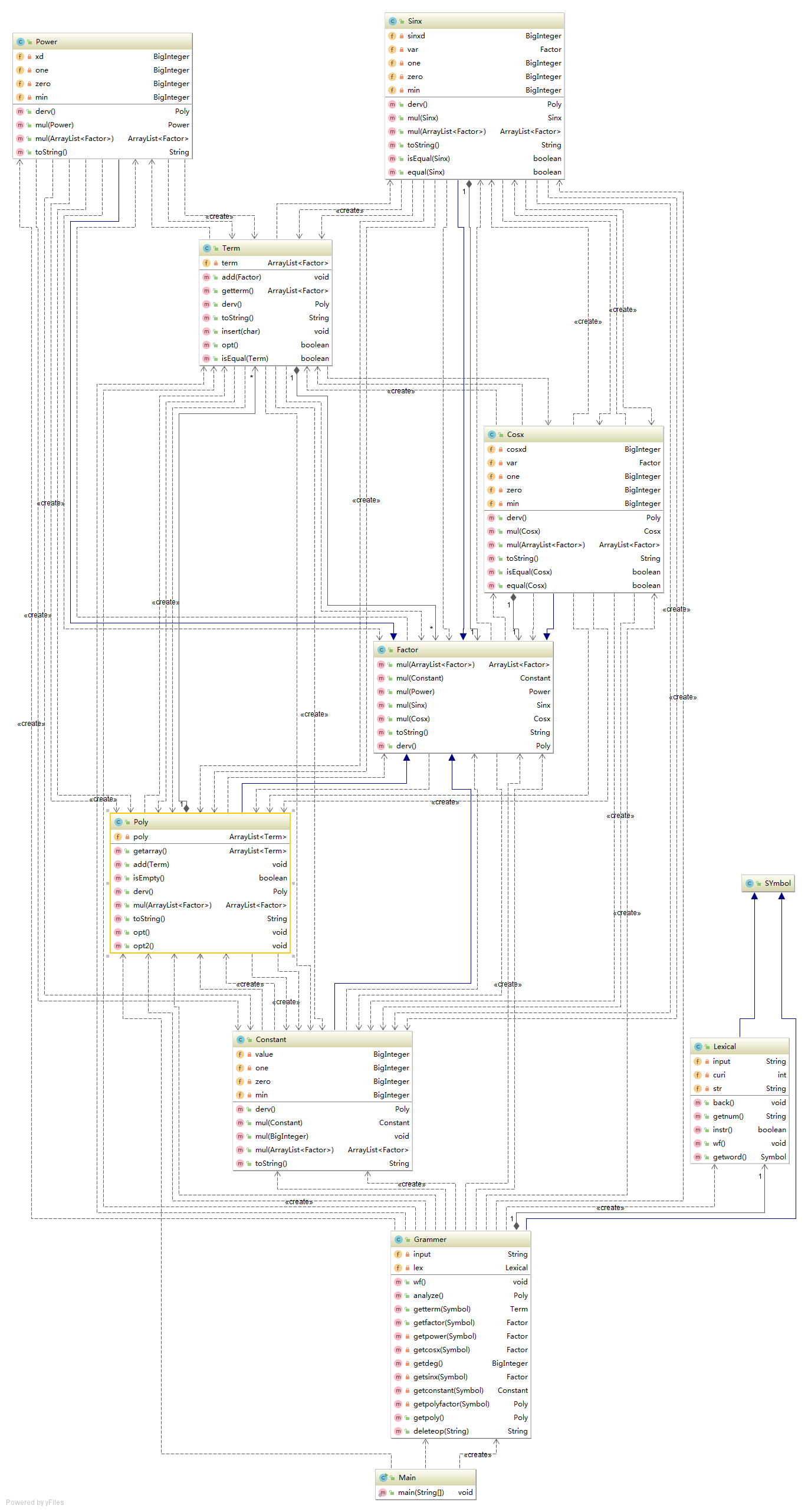
### **3.程序结构分析与总结**

​	首先，第三次oo作业我并没有采用第二次作业的正则表达式进行分析输入（因为一开始对于括号的正则担心匹配会爆栈，导致错误出现），所以我选择了上学期编译原理所使用的**词法分析和语法分析**来进行输入字符串的处理与分发工作，也就是我程序中的Grammer和Lexical这两个公共类所起到的作用。在写程序之前，通过研读指导书，我采用了**树形结构**进行储存多项式，即Poly是由多个Term组成，Term是由多个Factor组成，然后将因子进行不同类的划分与子类的方法实现，最终形成了我这次作业的整体架构。

​	优点：这次作业的架构在我的脑海中形成之后，在写程序的时候很方便的就进行一个模块一个模块的编写，写的时候只需要关注这个模块要实现的功能和流出的接口，所以相当于写一个一个黑箱，不需要在写的时候因为其他模块会有很大的更改（这应该就是**模块化**的优点），当写完一整个之后，各个模块之间的结构很好地拼接在了一起（虽然第一次运行出了很多bug）。这次作业的完成一大功劳要归于继承，由于这一次因子有很多个种类，特别是表达式因子的出现，导致第三次作业我的架构整体颠覆了第二次作业（第二次作业因子和项我作为一个东西，因为实际上无论多长的项都是（**a x^bsin(x)^c cos(x)^d**这种结构），这次作业将因子Factor作为父类，各个种类的因子进行单独实现方法与继承父类，由于java可以很好的分辨子类之间方法的运用，所以我们只需要实例化Factor就可以对于不同类的因子做一个整体性的运用，这大大减轻了对于不同因子的分别处理时间。

​	缺点：由于我java语言并不熟悉，所以这次作业我并没有很好地使用接口这个东西，而仅仅只是使用了继承，所以实际上可能我的类的方法实现并没有那么的合理，耦合性也有待提高。此外就是我的输入处理并没有采用推荐的正则表达式匹配（后来与同学探讨发现其实还是可以用的，只要在一开始对于括号的层次进行处理便可以很方便的用正则匹配了）。我的java程序有一个很大的缺点，就是美观性不够好，每一次写之前都希望能够写的紧凑和实用，但是一旦做到后面的复杂结构，都会用**冗余来代替思考**（也可以归结于菜），尤其是在写优化的时候，我就会在各个类进行优化方法的暴力添加~~尴尬的是这次作业我的优化得分惨不忍睹~~。

## （二）程序思考与分享

### **1.对于输入的处理**

```java
String pa1 = "([ \t]*)[+-]?\d+([ \t]*)";
String pa2 = "([ \t]*)x([ \t]*)(\^([ \t]*)[+-]?\d+)?([ \t]*)";
String pa3 = "([ \t]*)(sin([ \t]*)\(([ \t]*)x([ \t]*)\)|cos([ \t]*)\(([ \t]*)x([ \t]*)\))([ \t]*)(\^([ \t]*)[+-]?\d+)?([ \t]*)";
String pafac = "(" + pa3 + "|" + pa2 + "|" + pa1 + ")";
String pafache = "([+-]?" + pa3 + "|[+-]?" + pa2 + "|[+-]?" + pa1 + ")";
String paterm = "(" + pafache + "(([ \t]*)\*([ \t]*)" + pafac + ")*" + ")";
String pahead = "([ \t]*)[+-]?[ \t]*" + paterm;
String pa = "([ \t]*)[+-][ \t]*" + paterm;

第二次作业采用了完全正则匹配，我的做法是将因子划分成三种形式的正则，然后对于匹配的头部和后部进行分别分析，然后拼接组装成最后的正则匹配串。（这里特别提一点，我觉得使用\S*不应该作为考察错误点出现，这个实际上没有什么考察价值吧）

String[] wfpa = new String[8];
wfpa[0] = "\*[ \t]*[+-][ \t]+[0-9]";
wfpa[1] = "[+-][ \t]*[+-][ \t]*[+-][ \t]+[0-9]";
wfpa[2] = "s[ \t]+i[ \t]*n";
wfpa[3] = "s[ \t]*i[ \t]+n";
wfpa[4] = "c[ \t]+o[ \t]*s";
wfpa[5] = "c[ \t]*o[ \t]+s";
wfpa[6] = "\^[ \t]*\+[ \t]+[0-9]";
wfpa[7] = "[0-9][ \t]+[0-9]";
for (int i = 0; i < wfpa.length; i++) {
    Pattern pa = Pattern.compile(wfpa[i]);
    Matcher ma = pa.matcher(input);
    if (ma.find()) {
        System.out.println("WRONG FORMAT!");
        System.exit(0);
    }
}
input = input.replaceAll("[ \t]", "");

第三次作业由于一开始我觉得正则匹配多重嵌套括号会导致错误，所以我只是在一开始对于空格和TAB的错误出现位置进行了简易的正则匹配，然后把输入串进行消除空格和TAB，剩下其他的错误就交给词法分析和语法分析来进行处理，当然在语法分析的时候会进行字符串转换成表达式的各个部分的处理。

2.对于求导的处理

这里我也仅对于第二次和第三次作业进行阐述。

第二次作业

private BigInteger coe;
private BigInteger xd;
private BigInteger sinxd;
private BigInteger cosxd;

在第二次作业中，由于只会出现sin(x)和cos(x)，所以其实如果我们在对于输入处理的时候把每次的因子进行整合，最后出现的形式是一个标准格式即

ax^b*sin(x)c*cos(x)^d

由于可以整合成一个标准格式，所以其实求导就是一个方法就可以解决的问题，我们可以写出一个求导规则进行计算机的求导实现，当然我们也可以使用MATLAB对于这个标准格式进行标准求导,那么我们就可以直接用公式计算系数（如果第二次作业用了这种方法，可以减少错误发生的概率）MATLAB求导结果如下所示：

abx^{b-1}*cos(x)dsin(x)^c+a*c*xbcos(x)cos(x)^d*sin(x){c-1}-adx^b*cos(x){d-1}sin(x)*sin(x)^c

第三次作业

由于第三次作业的求导相较于之前有了很大的难度提升，所以实现方法就是对于各个因子进行求导方法的实现（包括链式法则），在上层Term进行求导计算，也就是乘法部分的求导实现。（把指导书中这两种特殊求导贴在下面）

链式法则：[f(g(x))]' = f'(g(x))g'(x)

乘法：当f(x) = g(x)h(x)时，f'(x) = g'(x)h(x)+g(x)h'(x)

这两种求导的实现是对于自己写的因子类和项类的方法组合。这个时候我就要说明一下了，在实现类方法尤其是乘法求导这样的时候，最好不要对方法实现的主体进行修改，我都是采用一个方法生成一个新的实例进行返回，就算有的时候需要再整体的ArrayList上进行重新的SET方法，但是这样可以避免方法对于原先实体的破坏和丢失。

3.对于优化的处理

之前一直没提到的第一次作业这个时候就要说明一下了，在第一次作业的时候，我做了合并同类项和对一开始多项式值为0的消除，但是我忘了在求导完之后可能会出现的合并同类项后再次出现值为0的项这件事情，导致了第一次作业的几个点优化得分为0，当看到反馈结果是因为0*这种原因，确实让我十分懊悔。

对于第二次作业优化的方法有很多，在讨论区也引起的一阵热议，考虑的越多，越发现要找出一个最优的算法需要大量的工作实现，因为有的时候合并不一定是缩短，更可能是突如其来的增加，这使得我做的时候畏手畏脚，只敢去做我验证过无论什么情况都是一定缩短的合并项，这也导致我的优化并不好。但是，重点来了，当我看到了测试结果后，我发现考察的重点不是最优化算法的实现，而基本上考察的都是同种系数的合并，也就是不会出现合并增加的情况，也就是说，只要你去做了简单的覆盖面全的同系数三角函数合并，那么你优化就可以得到满分也就是告诉我们不要偷懒？，也就是以下三种合并方式：

asin(x)^2+acos(x)2=a

b-bsin(x)^2=bcos(x)2

c-ccos(x)^2=csin(x)

第三次作业的优化我个人认为就是对于结构的考察，如果结构的创建没有很好的考虑到优化的实现，那么你基本上优化就会成为一个全新的工作，你需要在你的框架上搭建每一个类的isEqual方法的实现，然后在每一个上层进行判断合并，就更不用说上层之间的合并了，那更是一个复杂的工作。对于我个人的结构，就是没有考虑优化，我在程序正确运行后，就是在架构上进行打孔和加光纤这样的工作，这样的工作会导致正确性的不确定性，所以优化也是需要DEBUG这个工作，我只做了输入的时候简单的各个层次的合并还有求导之后各个层级的合并，所以最后得到的优化分数也不到一半。

（三）自测与BUG

1.自测

对于自己的程序，在我写完之后，首先测试的是输入的WRONG FORMAT的检查，这个部分就靠自己对于指导书的理解，进行不同种输入的测试（特别是+-号的出现次数，可以参考我第二部分对于输入的处理中第三次作业的wf格式，这几种就是我总结的空格TAB出现错误的所有情况）。在进行完格式检查之后，我就会认定自己的格式没有问题，然后用java进行自己的正则表达式的随机生成，然后进行自己java求导的结果和正确求导结果的对拍，来进行对比之间的差异，当发现不同的时候，我就会进行拆分输入debug，将一个很长的串进行精准拆分分析来找出我程序的bug。

2.BUG

我的程序求导部分写的还算严谨，所以在正确性方面还是比较可靠，每一次的强侧都可以得到所有的正确性分数，但实际上我对于输入的理解还不到位，就拿第三次作业举例，在截止时间的前4个小时的时候，我打开我的程序，进行测试输入，正确的输入都获得了正确的结果，但是我定睛一看，发现我写的WF的匹配哪里不对劲，我考虑的是哪里不能出现空格TAB，好像哪里缺少了什么，啊，原来是这个格式我太关注于哪里不能出现，而忘了其他字符之间可能会出现空格TAB，这样我就少考虑了东西，我进行检验，发现果然考虑的少了，然后就进行了刺激的修补工作（截止时间前一段时间的修改会很没有安全感）例子在下面：

wfpa[1] = "[+-][+-][+-][ \t]+[0-9]";//修改前
wfpa[1] = "[+-][ \t]*[+-][ \t]*[+-][ \t]+[0-9]";//修改后

（因为1623没有互测部分，所以大部分工作都是对以自己代码的修改和与同学之间的讨论分析）

（四）整体性总结

1.工厂模式重构

如果使用工厂模式进行重构，那么具体的实现就会是因子Factor部分，我的结构里有Constant,Power,Sinx,Cosx，这四种子类。当进行工厂设计模式时，要创建Factor接口和实现Factor接口的实体类。

(1)创建接口

public interface Factor {
     void derv(){}
}

(2)创建实现接口的实体类

public class Constant implements Factor {
    public void derv(){}
}
public class Power implements Factor {
     public void derv(){}
}
public class Sinx implements Factor {
     public void derv(){}
}
public class Cosx implements Factor {
     public void derv(){}
}

(3)创建一个工厂，生成基于给定信息的实体类的对象

public class FactorFactory{
    public Factor getFactor(String FactorType){
      if(FactorType == null){
         return null;
      }        
      if(FactorType.equals("Constant")){
         return new Constant();
      } else if(FactorType.equals("Power")){
         return new Power();
      } else if(FactorType.equals("Sinx")){
         return new Sinx();
      } else if(FactorType.equals("Cosx")){
         return new Cosx();
      }
      return null;
   }
}

(4)使用该工厂，通过传递类型信息来获取实体类的对象。

 public static void main(String[] args) {
      FactorFactory factorFactory = new FactorFactory();
 
      //获取Constant的对象，并调用它的求导derv方法
      Factor Factor1 = factorFactory .getFactor("Constant");
     //调用Constant的求导derv方法
      Factor1.derv();

2.总结

第一部分的多项式求导任务给我这个JAVA菜鸟带来了不小的挑战，从一开始的基础多项式到后面的嵌套因子的求导，每一次的作业都是对于结构的升级（对于我来说就是对于结构的重构，基本都是全新的程序，因为我没有做到前瞻性）。表达式求导这个部分，我感觉就相当于去实现MATLAB中的diff()函数的基础功能，可以发现在进行第三次作业后，我们实际上就是搭建了一个求导的框架，我们实现了幂函数，简单三角函数还有常数的混合求导，但实际上由于继承类的应用，实际上可以增加更多种因子的子类，就比如反三角函数，我们需要实现的就仅仅是增加一个子类还有在这个子类相关功能，加上对于输入的处理就可以做到了。最后的最后，JAVA课程还是道阻且长啊苦笑。