题目描述
http://codeforces.com/contest/1339/problem/C
给定一个长度为 (n) 的无序数组,你可以在第 (x) 秒进行一次下面的操作。
- 从数组选取任意个数字(也可以一个都不选),为他们全部都加上 (2^{x-1}) 。
询问你最少可以用多少秒,使得数组非降序排列。
解题
最快策略
首先简化一下问题,假设操作变成:第 (x) 秒,可以选取任意个数字,为他们全部都加上 (1) 。分析一下在这个条件下,可以达到最少秒数的策略。
- 假设我们有一个分布如下图的不规则序列。
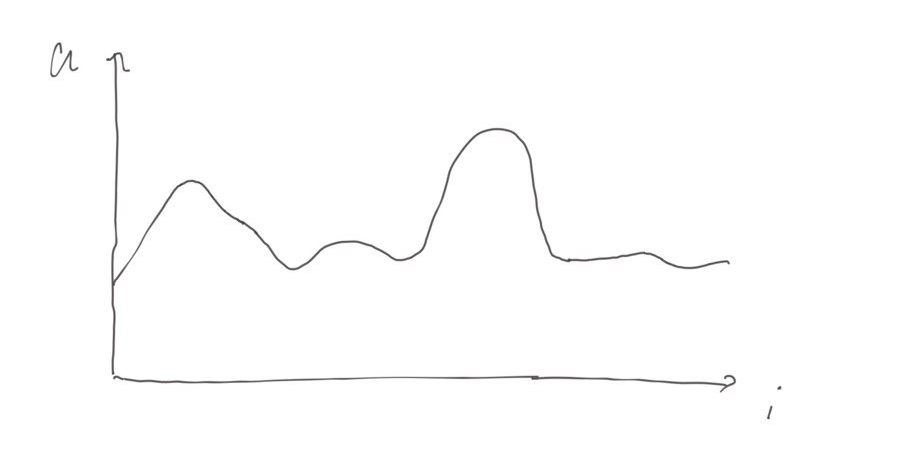
- 最快的让这个序列非降序排列的填充方案如图。

设对数字 (a_i) 加 (1) 的次数为 (d_i),可以不难发现 (d_i = max{a_j|jle i} - a_i) ,又因为每次 (+1) 操作是批量的,即每次可以选取多个 (a_i) 进行 (+1) 操作,所以最快策略的秒数花费 (ans = max{d_i|iin[1,n]}) 。
最终解题
同理,设对数字 (a_i) 加 (2^{x-1}) 的操作次数为 (d_i),
[d_i = left{ egin{array}{**lr**} sovle("max{a_j|jle i} - a_i = sum _{k=1}^{d_i}2^{k-1}")& ,max{a_j|jle i} - a_igt 0\\ 0& ,max{a_j|jle i} - a_i= 0\ end{array}
ight.
]
最后结果 (ans = max{d_i|iin [1,n]}) 。
#include<bits/stdc++.h>
#define ll long long
#define fr(i,n) for(int i=0;i<n;i++)
#define frs(i,n,flag) for(int i=0;i<n&&flag;i++)
#define frr(i,j,n) for(int i=j;i<n;i++)
#define r_frr(i,j,n) for(int i=n-1;i>=j;i--)
#define frrs(i,j,n,flag) for(int i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag) for(int i=n-1;i>=j&&flag;i--)
#define arend(i,n) ((i!=n-1)?" ":"
")
#define memset0(dp) memset(dp,0,sizeof(dp))
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<<arend(it,end);
#define log_this(name,value) cout<<name<<": "<<value<<endl;
#define e4 10004
#define e5 100005
#define e6 1000006
#define e7 10000007
#define e9 1000000000
#define INF 9999999
using namespace std;
int to_int(string s) {stringstream ss;ss<<s;int a;ss>>a;return a;}
string to_str(double a) {stringstream ss;ss<<a;return ss.str();}
ll a[1*e5];
int main(){
cin.tie(0);
//ios::sync_with_stdio(false);
//cout<<setiosflags(ios::fixed)<<setprecision(0);
//freopen("1.out","w",stdout);
int t;
while(cin>>t){
while(t--){
int n;
cin>>n;
fr(i,n){
cin>>a[i];
}
ll pr = 0;
ll maxa = a[0];
fr(i,n-1){
maxa = max(maxa,a[i+1]);
pr = max(pr,maxa-a[i+1]);
}
ll x = 0;
ll pw = 1;
while(pr>0){
pr -= pw;
pw *= 2;
x++;
}
cout<<x<<endl;
}
}
return 0;
}