题目描述
小仓鼠的和他的基(mei)友(zi)sugar住在地下洞穴中,每个节点的编号为1~n。地下洞穴是一个树形结构。这一天小仓鼠打算从从他的卧室(a)到餐厅(b),而他的基友同时要从他的卧室(c)到图书馆(d)。他们都会走最短路径。现在小仓鼠希望知道,有没有可能在某个地方,可以碰到他的基友?
小仓鼠那么弱,还要天天被zzq大爷虐,请你快来救救他吧!
解析
当然可以树剖。
一开始想用路径长作为判断依据,但总是WA,下数据发现就错那么一个两个小问,也是很玄学。。。
于是转而研究点如何作为判断依据。
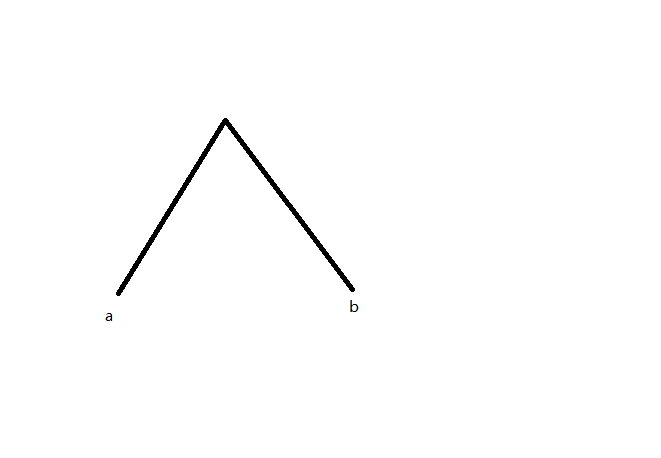
对于一个这样的树链,它的两端点为(a,b),如下图。
反过来想,如果我们要构造一条路径,使得树上某一个点到另一点的路径与现有路径相交,该如何做呢?
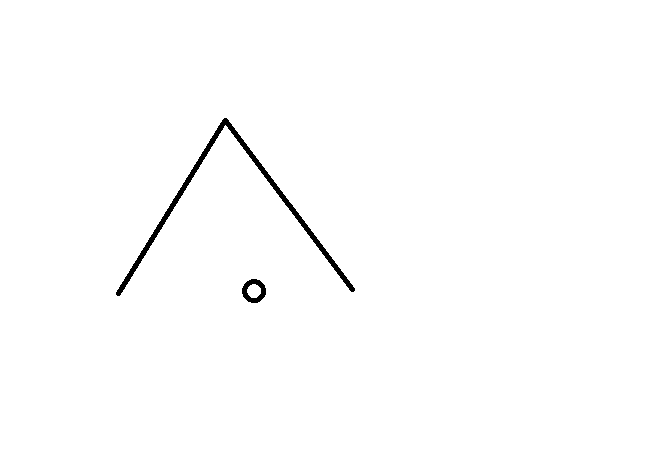
首先,这个点肯定要先有一部分路径连到原先的树链上吧,否则不可能相交。
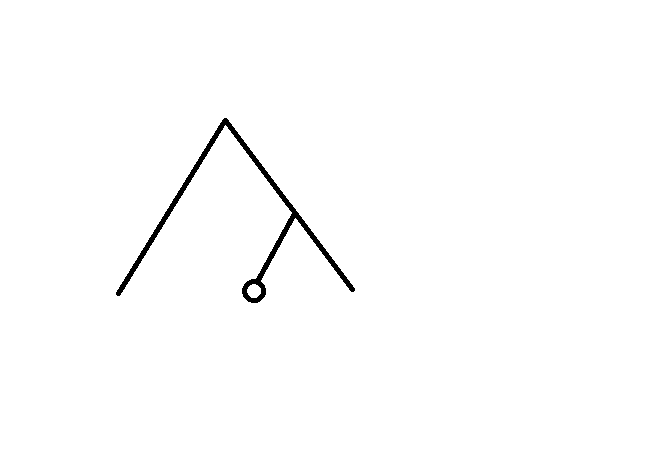
构造出的路径剩下的部分只可能是这三种情况。
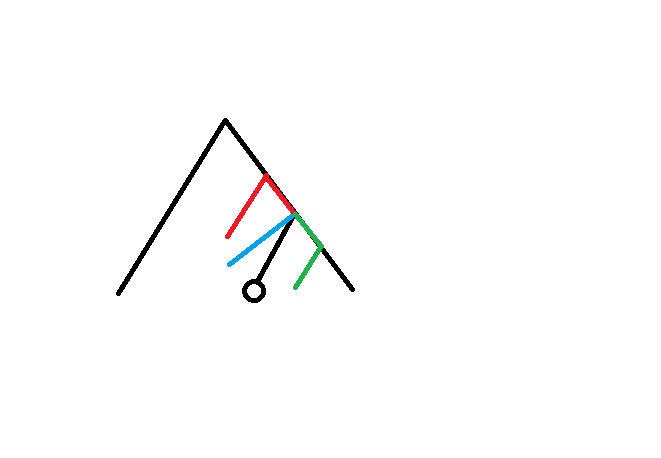
而如果这样构造路径就违反了树的定义。
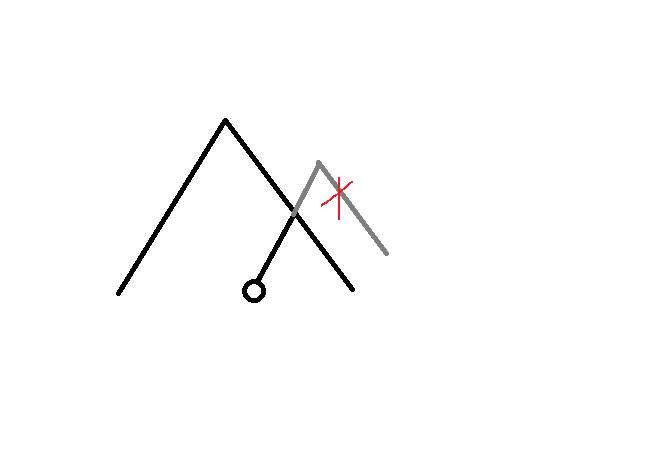
我们发现,构造出的路径一定有一个点在原树链上。但是这样还是不好下手,我们并不知道如何寻找这个点。
再进一步观察,发现新路径两端点的lca一定在原树链上。而lca很容易求,爱怎么求怎么求。
因此对于原问题,我们只需要判断某一对点的lca是否在另一对点表示的树链上即可。
判断一个点是否在一条树链上很容易,如果有一个点(x),我们要判断它是否在(a,b)构成的树链
((a,b))上,显然若
[deep[x]>=deep[lca(a,b)]&&(lca(a,x)==x| lca(b,x)==x)
]
成立,那么(x)在((a,b))上。
参考代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 100010
#define MOD 2520
#define E 1e-12
using namespace std;
inline int read()
{
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct rec{
int next,ver;
}g[N<<1];
int head[N],tot;
inline void add(int x,int y)
{
g[++tot].ver=y;
g[tot].next=head[x],head[x]=tot;
}
int f[21][N],dep[N],n,t;
inline void init()
{
queue<int> q;
q.push(1);dep[1]=1;
while(q.size()){
int x=q.front();q.pop();
for(int i=head[x];i;i=g[i].next){
int y=g[i].ver;
if(dep[y]) continue;
f[0][y]=x;dep[y]=dep[x]+1;
for(int j=1;j<=t;++j)
f[j][y]=f[j-1][f[j-1][y]];
q.push(y);
}
}
}
inline int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int j=t;j>=0;--j)
if(dep[f[j][x]]>=dep[y]) x=f[j][x];
if(x==y) return x;
for(int j=t;j>=0;--j)
if(f[j][x]!=f[j][y]) x=f[j][x],y=f[j][y];
return f[0][x];
}
int main()
{
int q;
n=read(),q=read();t=log2(n)+1;
for(int i=1;i<n;++i){
int u=read(),v=read();
add(u,v),add(v,u);
}
init();
while(q--){
int a=read(),b=read(),c=read(),d=read();
int k1=lca(a,b),k2=lca(c,d);
if(dep[k1]>=dep[k2]&&(lca(c,k1)==k1||lca(d,k1)==k1)) puts("Y");
else if(dep[k2]>=dep[k1]&&(lca(a,k2)==k2||lca(b,k2)==k2)) puts("Y");
else puts("N");
}
return 0;
}