【线头DP】JZOJ3320.【BOI2013】【LOJ#2687 Vim】文本编辑器

Description

N<=7e4,字符集为’a’~'j’共10个

Solution

• 暴力（N³）

• 比赛的时候题意没有看清楚，但是暴力的思路还是正确的，却因为我没有看清f操作代价为2，而删除一个e后向右移，所以惨爆零。

• 先来看一看比较显然的策略，我们每一次都是一直往后跳到某个位置（称向左为向前，向右即为向后），再一直往前跳并删去这一段中的e，所以每一次e是一段一段地被删去的。

• 因为我们可以发现我们到某个位置一定是一直往后跳，过程中往前一定不优。

• 然后我们是可以从后往前删去e的，所以就可以一段一段地删。

• 所以以上的策略是成立的。我们不难设一个状态f[i][j]表示删完了前i个e，当前光标的位置在j的最小代价。然后枚举下一个e，通过一些预处理可以把这些代价算出来。所以就完成了n³的DP。

• 线头DP（n*|字符集大小|²）

• 一个十分神奇的DP。借鉴了网上的两篇博客(https://www.cnblogs.com/Itst/p/10339605.html)
  (https://www.cnblogs.com/cjyyb/p/11146822.html)

• DP方程比较长这里就不再赘述。它的含义大家就请看着两篇博客，写的十分详细，并且配有图。在此我只说一下自己的一些理解。

• 我们将e去掉之后留有一些关键点，我们有两种走法，要么向后走，要么向前走，并且要求走到所有的关键点。根据我们暴力中的策略，我们的走法中一段i-(i+1)的边要么被覆盖1次，要么被覆盖3次。

• 现在我们要根据这种路径的特点构造出一个没有后效性并且可以单一表示的状态。

• 于是就有了f[i][j]表示覆盖一次i-(i+1)，g[i][j][k]表示覆盖三次i-(i+1)。

• 在理解状态的意义之后我们需要注意到对于任意一个f[i][j]或g[i][j][k]，所谓的代价实际上是1-i每个节点向后跳的边和1-(i+1)每个节点向前走的代价之和。也就是对于一个位置i横切下来再路径上的左边所有的代价之和。
  

• 所以我们在构造这个路径的时候，实际上是考虑将这条路径延长，或者将前面的点和后面的点（我们有往后跳的边）连接起来，并考虑它的贡献。

• 也许你会问有一个转移：
  g [ i ][ j ][ k ] = min ( f [ i - 1 ][ j ] + 3 )
  
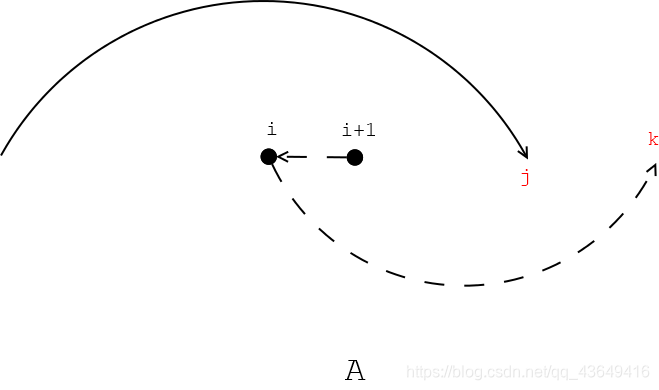
  上面i+1到j的路径的贡献为什么不算呢？

• 因为我们的状态设定的是i以前的代价，i+1到以后的关当前状态什么事呢？这一部分的代价会在之后转移的时候计算。

• 所以这整个DP实际上就是根据当前的路径（也许前后还没连起来）的形态进行转移。

• 最终要处理一下末尾的答案的一些细节，主要是考虑到线头DP要首位相连的性质（感性理解一波）。

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#define maxn 70005
#define maxs 11
using namespace std;

int n,i,j,k,len,cnt,a[maxn],imp[maxn],bz;
int f[maxn][maxs],g[maxn][maxs][maxs];
char ch;

void Min(int &x,int y){x=min(x,y);}

int main(){
	scanf("%d",&n);
	for(ch=getchar();ch<'a'||ch>'j';ch=getchar());
	bz=0;
	for(i=1;i<=n;i++){
		if (ch!='e') a[++len]=ch-'a',imp[len]=bz,bz=0;
		else bz=1,cnt++;
		ch=getchar();
	}
	memset(f,127,sizeof(f));
	memset(g,127,sizeof(g));
	f[0][a[1]]=0;
	for(i=1;i<=len;i++) {
		for(j=0;j<10;j++) {
			if (!imp[i]&&j!=a[i]) Min(f[i][j],f[i-1][j]);
			Min(f[i][j],f[i-1][a[i]]+2);
			if (j!=a[i]) Min(f[i][j],g[i-1][a[i]][j]);
			Min(f[i][j],g[i-1][a[i]][a[i]]+2);
		}
		for(j=0;j<10;j++) for(k=0;k<10;k++){
			if (j!=a[i]) Min(g[i][j][k],f[i-1][j]+3);
			Min(g[i][j][k],f[i-1][a[i]]+5);
			if (j!=a[i]&&k!=a[i]) Min(g[i][j][k],g[i-1][j][k]+1);
			if (k!=a[i]) Min(g[i][j][k],g[i-1][a[i]][k]+3);
			if (j!=a[i]) Min(g[i][j][k],g[i-1][j][a[i]]+3);
			Min(g[i][j][k],g[i-1][a[i]][a[i]]+5);
		}
	}
	printf("%d",f[len]['e'-'a']+2*cnt-2);
}