首先,HHT中用到的EMD详细介绍:https://wenku.baidu.com/view/3bba7029b4daa58da0114a9a.html
本文具体参考
为什么要用EMD?
对于信号的处理,可以是在频域,时域,或者时频域,其中信号在时频处理的方法有小波变换和EMD,但是小波变换是基于指定小波基的分析,一旦指定小波基,就是的分解出来的模式固定,而对于不同信号的分析最好采用不同的小波基以达到最好的处理效果;对应的EMD的方法正好可以解决这个问题,EMD相当于是一种自适应正交基的时频信号处理方法。也就是说对于一段未知的非线性非平稳信号的处理,不需要预先的分析与研究,就可以直接开始分解,这个方法会自动按照一些固定模式按层次分好,不需要人为干预与设置。
要理解EMD方法,就需要理解分析本征模态分量IMF
IMF指的是原始信号被EMD分解后得到的各层信号分量,我们通常认为任何信号都可以分解成若干个IMF的分量之和,IMF有两个约束条件
(1)在整个数据段内,极值点和过零点的个数必须相等或者 相差最多不能超过一个
(2)任意时刻由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零
最后对于具体的EMD的分解过程
1)根据原始信号的上下极值点,分别画出上下包络线
2)求上下包络线的均值,画出均值包络线
3)原始信号减均值包络线,得到中间信号
4)判断该中间信号是否是IMF(用上面的那两个条件)如果不是以该信号为基础重做1-4的分析
5)用上面的方法得到第一个IMF后,用原始信号减IMF1 作为新的原始信号, 再通过1-4的分析,可以得到IMF2,以此类推,完成EMD分解
在具体的应用中需要注意的是EMD分解过程中涉及到的:求解包络线的时候端点效应,以及筛分过程和分解过程的停止准则
实际信号中一旦出现间歇性信号,采用EMD的分解方法会出现频率混叠的现象,也叫模态混叠,具体的表现为一个IMF分量中存在多个尺度成分,或者是一个尺度成分在多个IMF分量中存在。
为了解决这个问题,人们提出了采用噪声辅助处理方法,EEMD(总体经验模态分解)以及CEEMD(补充总体经验模态分解)。EEMD是在原始信号中加入白噪声从而改变信号的极值点分布,而CEEMD则是在原始信号中加入一组噪声信号来改变信号的极值点分布。

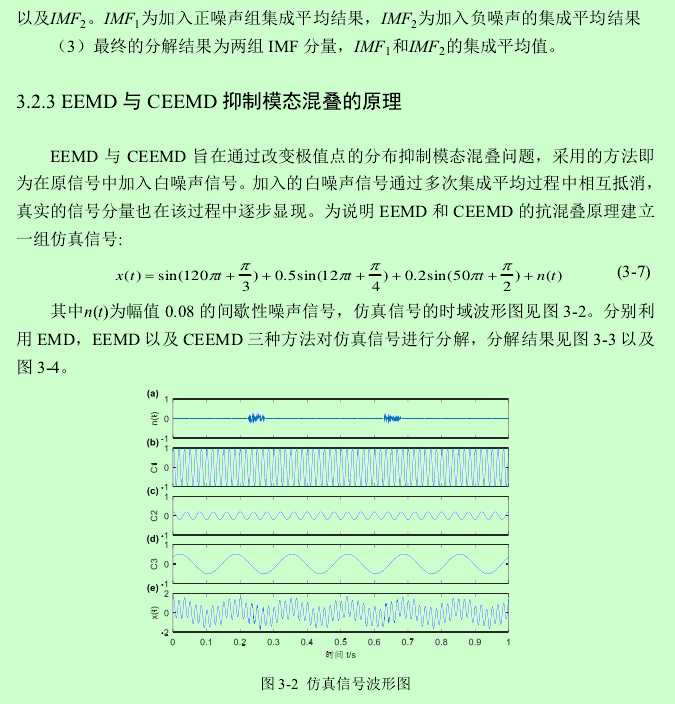
根据 Yeh 等人的研究,在加入相同数量以及相同幅值的白噪声时,EEMD 剩余噪声会随着集成平均的次数而逐渐减小。CEEMD 的剩余噪声一直维持在一个较小的程度,不论集成平均次数多少。在一定程度上使用 CEEMD方法进行信号分解,可以使用相对较少的集成平均次数,从某种意义上来说,CEEMD在保证小剩余噪声干扰的情况下,能够节省计算时间。