一.一些排序
1.快排递归
以下出自《编写高质量代码改善python程序的91个建议》
比如在Wikipedia的快速排序 条目中有如下伪代码:
伪代码
function quicksort('array')
if length('array') ≤ 1
return 'array' // an array of zero or one elements is already sorted
select and remove a pivot element 'pivot' from 'array' // see 'Choice of pivot' below
create empty lists 'less' and 'greater'
for each 'x' in 'array'
if 'x' ≤ 'pivot' then append 'x' to 'less'
else append 'x' to 'greater'
return concatenate(quicksort('less'), list('pivot'), quicksort('greater'))
// two recursive calls
实际上,它可以转化为以下同等行数的可以执行的Python代码:
python代码
def quicksort(array):
less = []; greater = []
if len(array) <= 1:
return array
pivot = array.pop()
for x in array:
if x <= pivot: less.append(x)
else: greater.append(x)
return quicksort(less)+[pivot]+quicksort(greater)
看,行数一样的Python代码甚至可读性比伪代码还要好吧?但它真的可以运行,结果如下:
>>>quicksort([9,8,4,5,32,64,2,1,0,10,19,27])
[0,1,2,4,5,8,9,10,19,27,32,64]
所以,综合这个例子来说,Pythonic也许可以定义为:充分体现Python自身特色的代码风格。
让之前不会快排的我,感觉到了,竟然这么简单能实现,知识从未如此简单易懂。了不起。其他的不懂的知识也应该可以找到简单的实现或者更容易理解的解释,然后让很多看起来很难的变得简单,会了就不难了。自己要快去发现或者去试着写写。让知识变得更简单易懂真是需要功力,加油,找到最简单的解。网上的版本,有点多,容易劝退,程序与程序之间还是有很多差异的,怪不得说要pythonic,要写的优雅易懂。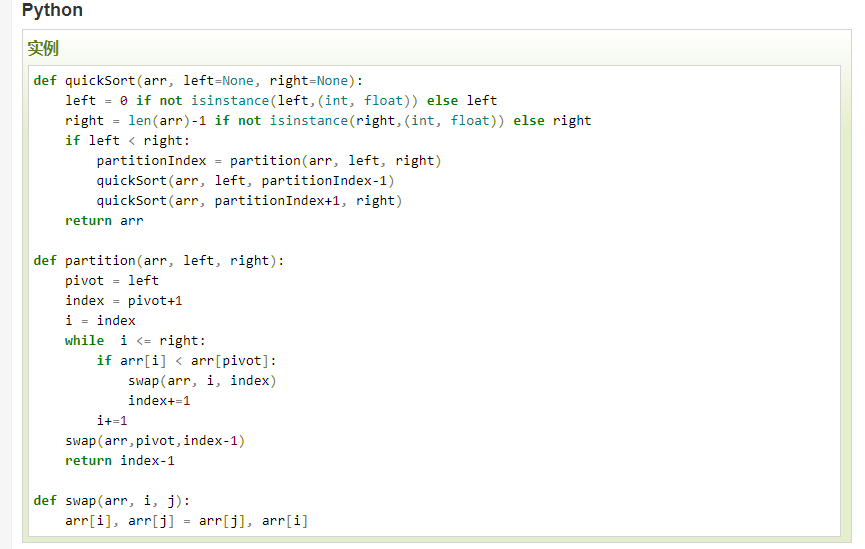
简单理解就是把要排序的列表最后一个元素取出,然后循环所有的元素,比他大的放右边列表、比他小的放左边列表,然后把两列表和中间值加起来。左右两个列表各自进函数排序。

完了,这个图画的不好,感觉复杂也没说不清楚,算了,先这样吧,在截图里不太好画。
看下网上的快排解释:
https://www.runoob.com/w3cnote/quick-sort-2.html
https://cloud.tencent.com/developer/article/1641537
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。#确实,一直往下分,就像一个大的工作,中分给下面两个,下面两个也往下分,直到没法分了 快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
为什么叫快排?因为快。为什么快?↓
*快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。*
平摊期望时间
https://www.cnblogs.com/lzr5350109/p/14836318.html
均摊(摊余)时间复杂度(amortized time complexity)
然而一些(最坏)时间复杂度表现不佳的算法,在实际应用中却依然有不错的表现。
这种类型算法的特点是:虽然单次操作的时间复杂度较高,但是单次操作后会对整个数据的组成状况带来一定的改进,因而后续的的系列操作时间复杂度会下降。这样最坏时间复杂度就不会在系列操作中连续出现,也就使得算法的实际运行时间并没有那么糟糕。
期望时间复杂度(expected time complexity)
有些时候,我们还会发现,一些系列操作时间复杂度高的算法,也可能会有很好的运行效果。
这类算法往往就是随机性算法(Randonmized Algorithm),其中就有大名鼎鼎的快速(选择)排序(quick sort)与快速选择(quick select)。他们的特点是在特殊情况下,最坏时间复杂度和均摊时间复杂度(均摊时间复杂度也是最坏均摊时间复杂度,考虑的是系列操作最坏的情况)都不佳,就是说单次操作和系列操作都可能花费很长时间。但是这种特殊情况出现的概率非常低,以至于在实际运行中几乎不可能出现。而在一般情况下,算法又表现得非常好。。。
为了合理评价这类算法,研究人员采用了期望时间复杂度(expected time complexity),也可以说是(加权)平均时间复杂度((weighted)average time complexity)。就是说一定数据规模下,我们计算出各种数据情况出现的可能性以及相应的算法时间复杂度,将可能性和复杂度相乘后求和,就得到了期望的时间复杂度。这里的可能性如果都取相同(#意思是各种数据都会取到相同比例),那就是平均时间复杂度。当然,可能性也可以根据不同的算法应用情况来确定,这样有时会得到不同的期望时间复杂度。
总的来说
(最坏)时间复杂度指的是算法单次运行可能出现的最长时间,也是最常用的时间复杂度,每次操作一定能满足。
均摊(摊余)时间复杂度指的是系列操作下最长运行时间平摊到单次操作下的均值,系列操作下的总时间一定能满足。
期望时间复杂度指的是各种数据输入下算法的运行时间按概率求得的一个平均理想值,在大多情况下能满足(实际也够用了)。。。
表面上看这几个复杂度的严格程度是一个不如一个,但实际上这是在计算机从理论走向实际大规模应用的发展。一个算法好,理论分析上专家要说好,实际应用中群众也要说好,而实际的应用场景往往会和严格理论分析下的假定有所差别。
https://www.cnblogs.com/fanyi0922/p/10779471.html
2.好奇python内部sorted是基于什么排序
搜了下: