原题链接在这里:https://leetcode.com/problems/out-of-boundary-paths/description/
题目:
There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.
Example 1:
Input:m = 2, n = 2, N = 2, i = 0, j = 0 Output: 6 Explanation:
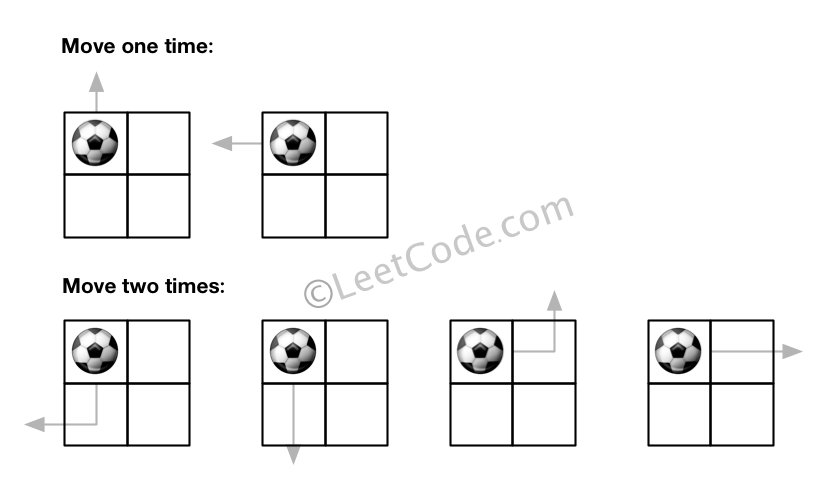
Example 2:
Input:m = 1, n = 3, N = 3, i = 0, j = 1 Output: 12 Explanation:
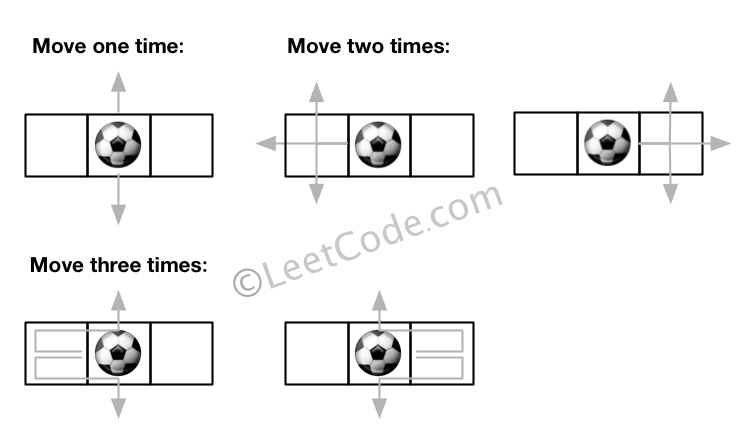
Note:
- Once you move the ball out of boundary, you cannot move it back.
- The length and height of the grid is in range [1,50].
- N is in range [0,50].
题解:
DP问题.
初始化dp[x][y]表示到x,y这个位置上有多少种走法. 刚开始给的 i, j 位置上是1, 其他位置全是0.
状态转移 (x,y) 从上下左右四个方向 往外走,走到dx, dy. dp[x][y] 就加到dp[dx][dy]上.
如果(dx, dy)已经出界了, 那说明这就是提出boundary了. 可以把dp[x][y] 加到res中.
答案是在每一种状态时边界点能从不同方向走出来的和.
Note: 角上只有一个点, 但可以从不同方向走出来,每个方向都要算一次.
Time Complexity: O(N*m*n).
Space: O(m*n).
AC Java:
1 class Solution { 2 public int findPaths(int m, int n, int N, int i, int j) { 3 int mod = 1000000007; 4 int [][] dp = new int[m][n]; 5 dp[i][j] = 1; 6 int res = 0; 7 int [][] dirs = {{-1,0},{1,0},{0,-1},{0,1}}; 8 9 for(int move = 0; move<N; move++){ 10 int [][] temp = new int[m][n]; 11 for(int x = 0; x<m; x++){ 12 for(int y = 0; y<n; y++){ 13 for(int [] dir : dirs){ 14 int dx = x+dir[0]; 15 int dy = y+dir[1]; 16 if(dx<0 || dx==m || dy<0 || dy==n){ 17 res = (res+dp[x][y])%mod; 18 }else{ 19 temp[dx][dy] = (temp[dx][dy]+dp[x][y])%mod; 20 } 21 } 22 } 23 } 24 dp = temp; 25 } 26 return res; 27 } 28 }