niop2015day2

P2678 跳石头

题目描述

这项比赛将在一条笔直的河道中进行，河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间，有 NN 块岩石（不含起点和终点的岩石）。在比赛过程中，选手们将从起点出发，每一步跳向相邻的岩石，直至到达终点。

为了提高比赛难度，组委会计划移走一些岩石，使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制，组委会至多从起点和终点之间移走 MM 块岩石（不能移走起点和终点的岩石）。

输入输出格式

输入格式：

输入文件第一行包含三个整数 L,N,ML,N,M ，分别表示起点到终点的距离，起点和终点之间的岩石数，以及组委会至多移走的岩石数。保证 L geq 1L≥1 且 N geq M geq 0N≥M≥0 。

接下来 NN 行，每行一个整数，第 ii 行的整数 $D_i（ 0 < D_i < L）$ ， 表示第 ii 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出，且不会有两个岩石出现在同一个位置。

输出格式：

输出文件只包含一个整数，即最短跳跃距离的最大值。

输入输出样例

输入样例#1： 复制

25 5 2 
2
11
14
17 
21

输出样例#1： 复制

4

说明

输入输出样例 1 说明：将与起点距离为 2 和 14 的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。

另：对于 20%的数据,0 ≤ M ≤ N ≤ 10。 对于50%的数据,0 ≤ M ≤ N ≤ 100。

对于 100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。

题解：二分距离

#include <bits/stdc++.h>

using namespace std;
const int maxn = 50005;
int dis[maxn];
int L, M, N;
bool check(int k){
    int t = 0, las = 0;
    for(int i = 1; i <= N+1; i++){
        if(dis[i] - las < k)
            t++;
        else las = dis[i];
        if(t > M)return 0;
    }

    return 1;
}
int main()
{
    //freopen("stone.in","r",stdin);
    //freopen("stone.out","w",stdout);
    int ans;
    scanf("%d%d%d",&L,&N,&M);
    for(int i = 1; i <= N; i++)scanf("%d",&dis[i]);
    dis[N+1] = L;
    int lf = 0, rg = L;
    while(lf <= rg){
        int mid = (lf + rg) >> 1;
        if(check(mid))ans = mid, lf = mid + 1;
        else rg = mid - 1;

    }
    printf("%d
",ans);
    return 0;
}

P2679 子串

题目描述

有两个仅包含小写英文字母的字符串 AA 和 BB 。

现在要从字符串 AA 中取出 kk 个互不重叠的非空子串，然后把这 kk 个子串按照其在字符串 AA 中出现的顺序依次连接起来得到一个新的字符串。请问有多少种方案可以使得这个新串与字符串 BB 相等？

注意：子串取出的位置不同也认为是不同的方案。

输入输出格式

输入格式：

第一行是三个正整数 n,m,kn,m,k ，分别表示字符串 AA 的长度，字符串 BB 的长度，以及问题描述中所提到的 kk ，每两个整数之间用一个空格隔开。

第二行包含一个长度为 nn 的字符串，表示字符串 AA 。

第三行包含一个长度为 mm 的字符串，表示字符串 BB 。

输出格式：

输出共一行，包含一个整数，表示所求方案数。

由于答案可能很大，所以这里要求输出答案对 10000000071000000007 取模的结果。

输入输出样例

输入样例#1： 复制

6 3 1 
aabaab 
aab

输出样例#1： 复制

2

输入样例#2： 复制

6 3 2 
aabaab 
aab

输出样例#2： 复制

7

输入样例#3： 复制

6 3 3 
aabaab 
aab

输出样例#3： 复制

7

说明

对于第 1 组数据:1≤n≤500,1≤m≤50,k=1;
对于第 2 组至第 3 组数据:1≤n≤500,1≤m≤50,k=2;
对于第 4 组至第 5 组数据:1≤n≤500,1≤m≤50,k=m;
对于第 1 组至第 7 组数据:1≤n≤500,1≤m≤50,1≤k≤m;
对于第 1 组至第 9 组数据:1≤n≤1000,1≤m≤100,1≤k≤m；

对于所有 10 组数据:1≤n≤1000,1≤m≤200,1≤k≤m。

题解：dp;果然又没想出方程

先想到： dp[ i ][ j ][ k ] = dp[ i-1 ][ j-1 ][ k ] + dp[ i-1 ][ j-1 ][ k-1 ]； ( A[i] == B[j] )

即：能匹配时，方案数为：单独使用当前字符为一个子串 + 与前面相连形成一个子串;

稍微仔细一想就可以知道，这个DP式子是有问题的，如果不使用当前字符被遗漏了

所以：

设s[ i ][ j ][ k ]为A到了 i ，B到了 j ，已经用了 k 个子串， 并且一定用了当前字符(A[i])时的方案数。

设f[ i ][ j ][ k ]为A到了 i ，B到了 j ，已经用了 k 个子串， 无论用不用当前字符(A[i])时的方案数总和。

能转移的前提自然是 A[ i ] == B [ j ]啦。

既然 A[i] 一定要用，那么依旧是两种情况：独自成一串 或 与前面的成一串。

s[ i ][ j ][ k ] = f[ i-1 ][ j-1 ][ k-1 ] + s[ i-1 ][ j-1 ][ k ]；

f[ i ][ j ][ k ] 的来源也有两种： 使用当前字符 或 不使用当前字符

 f[ i ][ j ][ k ] = f[ i-1 ][ j ][ k ] + s[ i ][ j ][ k ]；

然后由于空间原因开滚动数组，注意中间转移时A[i]！=B[j] f 要赋值0，不然会影响后面 

初始化 f[ i ][ 0 ][ 0 ] = 1, 不选也是一种方案

#include <bits/stdc++.h>

using namespace std;
int f[2][505][505], s[2][505][505];
char a[1005], b[1005];
const int M = 1000000007;
int main()
{
    //freopen("substring.in","r",stdin);
    //freopen("substring.out","w",stdout);
    int n, m, k, ans = 0;
    scanf("%d%d%d",&n,&m,&k);
    scanf("%s%s",a+1,b+1);
    int u = 0;
    f[0][0][0]=1;
    for(int i = 1; i <= n; i++){
        u^=1;
        f[u][0][0] = 1;
        for(int j = 1; j <= m; j++)
        for(int kk = 1; kk <= k; kk++){
            if(a[i] == b[j])s[u][j][kk] = (f[u^1][j-1][kk-1] + s[u^1][j-1][kk]) % M;
            else s[u][j][kk] = 0;
            f[u][j][kk] = (f[u^1][j][kk] + s[u][j][kk]) % M;
            //printf("%d %d %d %d %d
",i,j,kk,f[u][j][kk],s[u][j][kk]);
        }    
    }
    
    printf("%d
",f[u][m][k]);
    return 0;
}

P2680 运输计划

题目描述

公元 2044 年，人类进入了宇宙纪元。

L 国有 nn 个星球，还有 n-1n−1 条双向航道，每条航道建立在两个星球之间，这 n-1n−1 条航道连通了 LL 国的所有星球。

小 P 掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 u_iui​ 号星球沿最快的宇航路径飞行到 v_ivi​ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 jj ，任意飞船驶过它所花费的时间为 t_jtj​ ，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 mm 个运输计划。在虫洞建设完成后，这 mm 个运输计划会同时开始，所有飞船一起出发。当这 mm 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞， 试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入输出格式

输入格式：

第一行包括两个正整数 n, mn,m ，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 11 到 nn 编号。

接下来 n-1n−1 行描述航道的建设情况，其中第 ii 行包含三个整数 a_i, b_iai​,bi​ 和 t_iti​ ，表示第 ii 条双向航道修建在 a_iai​ 与 b_ibi​两个星球之间，任意飞船驶过它所花费的时间为 t_iti​ 。数据保证 1 leq a_i,b_i leq n1≤ai​,bi​≤n 且 0 leq t_i leq 10000≤ti​≤1000 。

接下来 mm 行描述运输计划的情况，其中第 jj 行包含两个正整数 u_juj​ 和 v_jvj​ ，表示第 jj 个运输计划是从 u_juj​ 号星球飞往 v_jvj​ 号星球。数据保证 1 leq u_i,v_i leq n1≤ui​,vi​≤n

输出格式：

输出文件只包含一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例#1： 复制

6 3 
1 2 3 
1 6 4 
3 1 7 
4 3 6 
3 5 5 
3 6 
2 5 
4 5

输出样例#1： 复制

11

说明

所有测试数据的范围和特点如下表所示

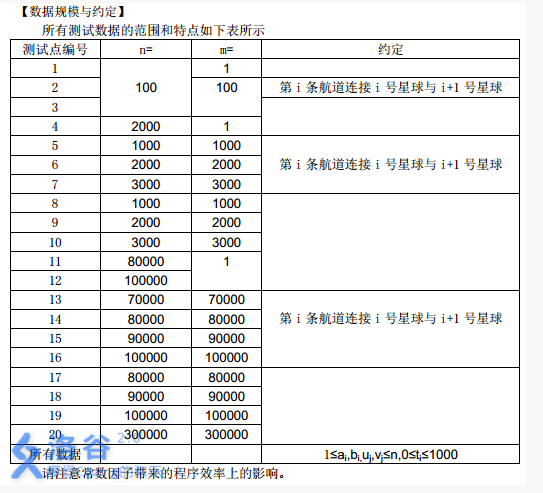
请注意常数因子带来的程序效率上的影响。

题解：先想到树剖+树状数组的暴力，每个点修改，复杂度N*M*LogN，会T

首先求出每个计划的路径长度 以及路径上的lca
然后二分时间k
统计 k<路径长的条数 cnt 并维护最大差值 rest 
并且对于每条不合法的路径维护每个点的经过次数
然后枚举点 如果经过次数==cnt说明每一条不合法的都经过他
然后尝试把它建成虫洞 如果他对应边的权值>=dec 那么我们删掉它ans就合法了
如果没有次数==cnt的，说明至少要建两个虫洞，直接舍掉
关键是统计每个点在非法路径中的经过次数 ：
维护sum数组 对于每个非法的路径起点a b LCA(a,b)==s sum[a]++ sum[b]++ sum[s]-=2//因为边权下放了点权
在dfs记录访问逆序，好一次更新，不然就N^2的

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int maxn = 300000+5, P = 20;
int Mtim, tot, idx;
int st[maxn], ed[maxn], anc[maxn][P+1], q[maxn], to[maxn];
int dep[maxn], dist[maxn], dis[maxn], h[maxn], du[maxn], lca[maxn];
struct edge{int v,w,nxt;}G[maxn<<1];
void add(int u,int v,int t){G[++tot].v = v;G[tot].w = t;G[tot].nxt = h[u]; h[u] = tot;}
void read(int &x){
    int f=1;x=0;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();}
    x*=f;
}
void dfs(int u, int fr){
    anc[u][0] = fr;
    for(int p = 1; p <= P; p++)
        anc[u][p] = anc[anc[u][p-1]][p-1];
    dep[u] = dep[fr] + 1;
    for(int i = h[u]; i; i = G[i].nxt){
        int v = G[i].v;
        if(v == fr)continue;
        to[v] = G[i].w;
        dis[v] = dis[u] + to[v];
        dfs(v, u);
    }
    q[++idx] = u;//访问逆序
}
int flca(int u, int v){
    if(dep[u] < dep[v])swap(u, v);
    int t = dep[u] - dep[v];
    for(int p=0; t; t>>=1, p++)
        if(t & 1)u = anc[u][p];
    if(u == v)return u;
    for(int p = P; p >= 0; p--)
        if(anc[u][p] != anc[v][p])
            u = anc[u][p], v = anc[v][p];
    return anc[u][0];
}
void init(){
    dfs(1, 0);
    for(int i = 1; i <= m; i++){
        lca[i] = flca(st[i], ed[i]);
        dist[i] = dis[st[i]] + dis[ed[i]] - 2*dis[lca[i]];
        Mtim = max(Mtim, dist[i]);
    }
}
bool check(int k){
    memset(du, 0, sizeof(du));//!
    int cnt = 0, rest = 0, hh = -1;
    for(int i = 1; i <= m; i++){
        if(dist[i] <= k)continue;
        cnt++;
        du[st[i]]++;du[ed[i]]++;
        du[lca[i]]-=2;
        rest = max(rest, dist[i] - k);
    }
    if(!cnt)return 1;
    for(int i = 1; i <= n; i++){
        int u = q[i];
        du[anc[u][0]] += du[u];
    }
    for(int i = 1; i <= n; i++)
        if(du[i] == cnt)hh = max(hh, to[i]);
    return rest <= hh;
}
void solve(){
    int lf = 0, rg = Mtim, ans = 0;
    while(lf <= rg){
        int mid = (lf + rg) >> 1;
        if(check(mid))ans = mid, rg = mid - 1;
        else lf = mid + 1;
    }
    printf("%d
",ans);
}
int main(){
   // freopen("transport.in","r",stdin);
   // freopen("transport.out","w",stdout);
    read(n),read(m);
    for(int i = 1; i < n; i++){
        int u, v, t;
        read(u),read(v),read(t);
        add(u,v,t);
        add(v,u,t);
    }
    for(int i = 1; i <= m; i++)
        read(st[i]), read(ed[i]);
    init();
    solve();
}