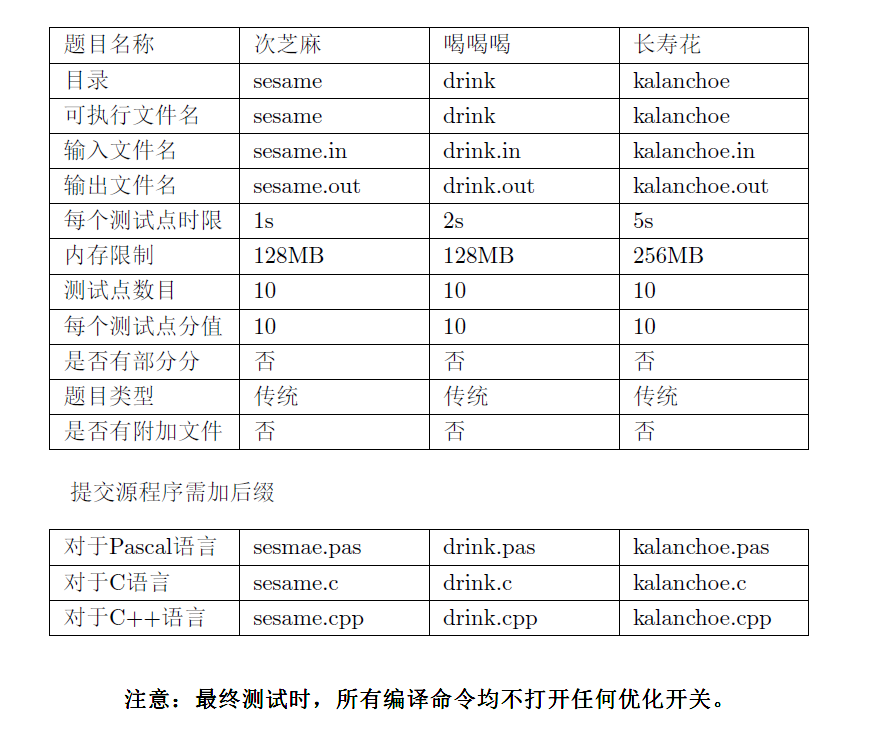




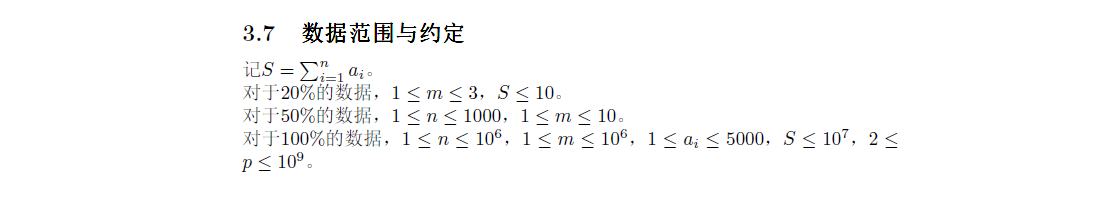
题解:
第一题:开始想找循环节,但数据很好卡; 后来想小的一直拿,那么另一个就会出现负数,抵消+打表发现就是2^k在mod(n+m)的值;

#include<bits/stdc++.h> using namespace std; #define ll long long ll mod, n, m; ll ksm(ll a, ll b){ ll ret = 1; for(; b; b >>= 1, a=a*a%mod) if(b&1) ret=ret*a%mod; return ret; } int main(){ freopen("sesame.in","r",stdin); freopen("sesame.out","w",stdout); ll k; cin>>n>>m>>k; mod = n + m; if(n > m) swap(n, m); ll ans = ksm(2, k); n = ans * n % mod; cout<<min(n, mod - n)<<endl; }
第二题:,Ax % Ay = k ==> Ax - k = n * Ay; 只需要判断(Ax - k)是否整除Ay即可,
ai <= 1e5; 利用这个性质想到拆分, 把Ax的因子都分解出来,如果他包含Ay,就记录一个max(now, lst),往后扫;
O(n√n)

#include<bits/stdc++.h> using namespace std; const int M = 1e5 + 10; #define ll long long int lst[M], a[M], k; void divi(int x, int pos){ for(int i = 1; i * i <= x; i++) if(x % i == 0) lst[i] = lst[x / i] = pos; } int main(){ freopen("drink.in","r",stdin); freopen("drink.out","w",stdout); int n, now = 0; ll ans = 0; scanf("%d%d", &n, &k); for(int i = 1; i <= n; i++) scanf("%d", &a[i]); for(int i = 1; i <= n; i++){ if(a[i] > k){ now = max(now, lst[0]); now = max(lst[a[i]], now); } ans = ans + 1LL*(i - now); if(a[i] - k >= k) divi(a[i] - k, i); else if(a[i] == k) lst[0] = i; //printf("%d %d ", now, i); } printf("%lld ", ans); }
第三题:利用ai<=5000 的性质,搞一个(ai^2), 题解附在代码中
#include<bits/stdc++.h> using namespace std; #define ll long long const int M = 5005; int f[M][M], a[1000005]; ll d[2][M], fac[M], P[M], mod; int main(){ freopen("kalanchoe.in","r",stdin); freopen("kalanchoe.out","w",stdout); int n, m; scanf("%d%d%lld", &n, &m, &mod); for(int i = 1; i <= n; i++)scanf("%d", a + i); f[1][1] = 1; for(int i = 2; i <= 5000; i++) for(int j = 1; j <= 5000; j++) f[i][j] = ((ll)f[i - 1][j - 1] + (ll)f[i - 1][j] * (j - 1) % mod ) % mod; //f[i][j] 表示有i个空位放j个颜色的方案数,可以选择放一个新的颜色或者原来的颜色 fac[0] = 1; P[1] = m; for(int i = 1; i <= 5000; i++) fac[i] = fac[i - 1] * i % mod; for(int i = 2; i <= 5000; i++) P[i] = P[i - 1] * (m - i + 1) % mod; // 排列 for(int i = 1; i <= a[1]; i++) d[1][i] = (ll)f[a[1]][i] * P[i] % mod; //d[i][j]表示第i行放j种颜色的方案数,f只确定了位置,放什么颜色排列 int u = 1; for(int i = 2; i <= n; i++){ u ^= 1; ll sum = 0; for(int j = 1; j <= a[i - 1]; j++) sum = (sum + d[u^1][j]) % mod; for(int j = 1; j <= a[i]; j++) { d[u][j] = (ll)f[a[i]][j] * P[j] % mod * sum % mod; //该行放j个的总方案数要乘上上一行的总方案数; if(j <= a[i - 1]) d[u][j] = ((d[u][j] - (ll)f[a[i]][j] * d[u^1][j] % mod * fac[j] % mod) + mod) % mod; //如果放的颜色比上一行总颜色种类少,那么可能会和上行颜色集合重复,我们强制这j种颜色和上行j种颜色同,怎么放就乘上fac[j] } } ll ans = 0; for(int i = 1; i <= a[n]; i++) ans = (ans + d[u][i]) % mod; printf("%lld ", ans); }
